Giải phương trình: 2+1x=(1x+2)(x2+1)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
26 tháng 4 2017
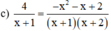
Điều kiện xác định: x ≠ -1; x ≠ -2.
Quy đồng và khử mẫu ta được:
4.(x + 2) = -x2 – x + 2
⇔ 4x + 8 = -x2 – x + 2
⇔ 4x + 8 + x2 + x – 2 = 0
⇔ x2 + 5x + 6 = 0.
Có a = 1; b = 5; c = 6 ⇒ Δ = 52 – 4.1.6 = 1 > 0
⇒ Phương trình có hai nghiệm phân biệt:
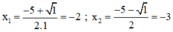
Chỉ có nghiệm x2 = -3 thỏa mãn điều kiện xác định.
Vậy phương trình có nghiệm x = -3.
PT
1
CM
3 tháng 9 2019
ĐKXĐ: x ≠ ± 1;x ≠ ± 2
Phương trình
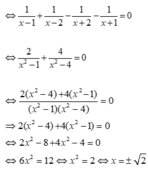
Vậy tập nghiệm của phương trình là S = { ± √ 2 }
CM
24 tháng 12 2017
1 x − x y = x 2 + x y − 2 y 2 ( 1 ) x + 3 − y 1 + x 2 + 3 x = 3 ( 2 )
Điều kiện: x > 0 y > 0 x + 3 ≥ 0 x 2 + 3 x ≥ 0 ⇔ x > 0 y > 0
( 1 ) ⇔ y − x y x = ( x − y ) ( x + 2 y ) ⇔ ( x − y ) x + 2 y + 1 y x = 0 ⇔ x = y do x + 2 y + 1 y x > 0 , ∀ x , y > 0
Thay y = x vào phương trình (2) ta được:
( x + 3 − x ) ( 1 + x 2 + 3 x ) = 3 ⇔ 1 + x 2 + 3 x = 3 x + 3 − x ⇔ 1 + x 2 + 3 x = x + 3 + x ⇔ x + 3 . x − x + 3 − x + 1 = 0 ⇔ ( x + 1 − 1 ) ( x − 1 ) = 0 ⇔ x + 3 = 1 x = 1 ⇔ x = − 2 ( L ) x = 1 ( t m ) ⇒ x = y = 1
Vậy hệ có nghiệm duy nhất (1;1)
CM
10 tháng 6 2018
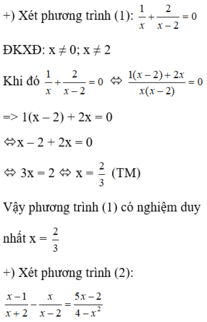
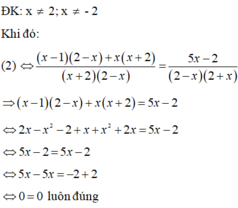
Vậy phương trình (2) có vô số nghiệm.
Do đó phương trình (2) có nhiều nghiệm hơn phương trình (1)
Chọn đáp án C
CM
3 tháng 4 2019
Điều kiện : x ≠ 3 và x ≠ -2
Ta có: x 2 - 3 x + 5 x - 3 x + 2 = 1 x - 3 ⇔ x 2 -3x +5 = x+2 ⇔ x 2 -4x +3 =0
Phương trình x 2 -4x +3 = 0 có a = 1 ,b = -4 , c = 3
Suy ra : a + b + c = 0
Ta có nghiệm x 1 =1 , x 2 =3 (loại)
Vậy nghiệm của phương trình là x = 1
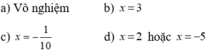
1/x 1/x và x ngũ 2
2 + 1x = (1x + 2)(x2 + 1)
<=> 2 + x = 2x2 + 2 + x3 + x
<=> x = 2x2 + x3 + x
<=> 0 = 2x2 + x3
<=> 2x2 + x3 = 0
<=> x2(2 + x) = 0
<=> x = 0 hoặc 2 + x = 0
<=> x = 0 hoặc x = -2