Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét tứ giác OBDM có
góc OBD+góc OMD=180 độ
=>OBDM là tư giác nội tiếp
c: Xét ΔKOB và ΔKFE có
góc KOB=góc KFE
góc OKB=góc FKE
=>ΔKOB đồng dạng với ΔKFE
=>KO/KF=KB/KE
=>KO*KE=KB*KF
a:
Xét (O) có
CM,CA là các tiếp tuyến
nên CM=CA và OC là phân giác của góc MOA(1)
mà OM=OA
nên OC là đường trung trực của MA
=>OC vuông góc với MA tại I
Xét (O) có
DM,DB là các tiếp tuyến
nên DM=DB và OD là phân giác của góc MOB(2)
mà OM=OB
nên OD là trung trực của BM
=>OD vuông góc với BM
Từ (1) và (2) suy ra góc COD=1/2*180=90 độ
b: AC*BD=MC*MD=MO^2=R^2
a. xét tứ giác OBMD có
∠DBO=90 ( tiếp tuyến By)
∠OMD=90 (tiếp tuyến tại M)
⇒∠DBO+∠OMD=90+90=180
⇒tứ giác OBMD nội tiếp
b.ΔOBF cân tại O do OB=OF=R
⇒∠B1=∠F1 (1)
có ∠E1=∠B1 (cùng phụ ∠EOB) (2)
từ (1);(2) ⇒∠F1=∠E1 (cùng nhìn OB)
⇒OFEB nội tiếp
⇒∠OFE=∠OBE=90
⇒EF⊥OF
⇒EF là tiếp tuyến của (O)
c. xét ΔKFO và ΔKEB có
∠FKO=∠EKB=90
∠E1=∠F1
⇒ΔKFO ∼ ΔKEB (g.g)
⇒\(\dfrac{KO}{KB}=\dfrac{KF}{KE}\)⇒KO.KE=KF.KB
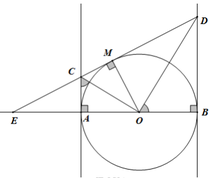
ta có tam giác ACDB có GTNN khi ACDB là hình chữ nhật
nối O với M . DỄ CHỨNG MINH ĐƯỢC ACMO VÀ OMDB LÀ HÌNH VUÔNG CẠNH R
suy ra diện tích ACM=1/2*AC*CM=1/2*AO*OM=1/2*R*R=\(\frac{R^2}{2}\)
TƯƠNG TỰ diện tích BDM=\(\frac{R^2}{2}\)
SUY RA TỔNG DIỆN TÍCH 2 TAM GIÁC LÀ \(\frac{R^2}{2}+\frac{R^2}{2}=\frac{2R^2}{2}=R^2\)
TICK NHA