Cho tam giác ABC nhọn ( AB < AC) có các đường cao AD, BE, CF cắt nhau tại H. Gọi M là điểm đối xứng của H qua D. Gọi I và K là hình chiếu của củ M trên AB và AC. Chứng minh a) góc AEF= góc CED.
b)Gọi N là gđ của EF và AM. C/m HN.AD=AN.DM
c) C/m I,D,K thẳng hàng

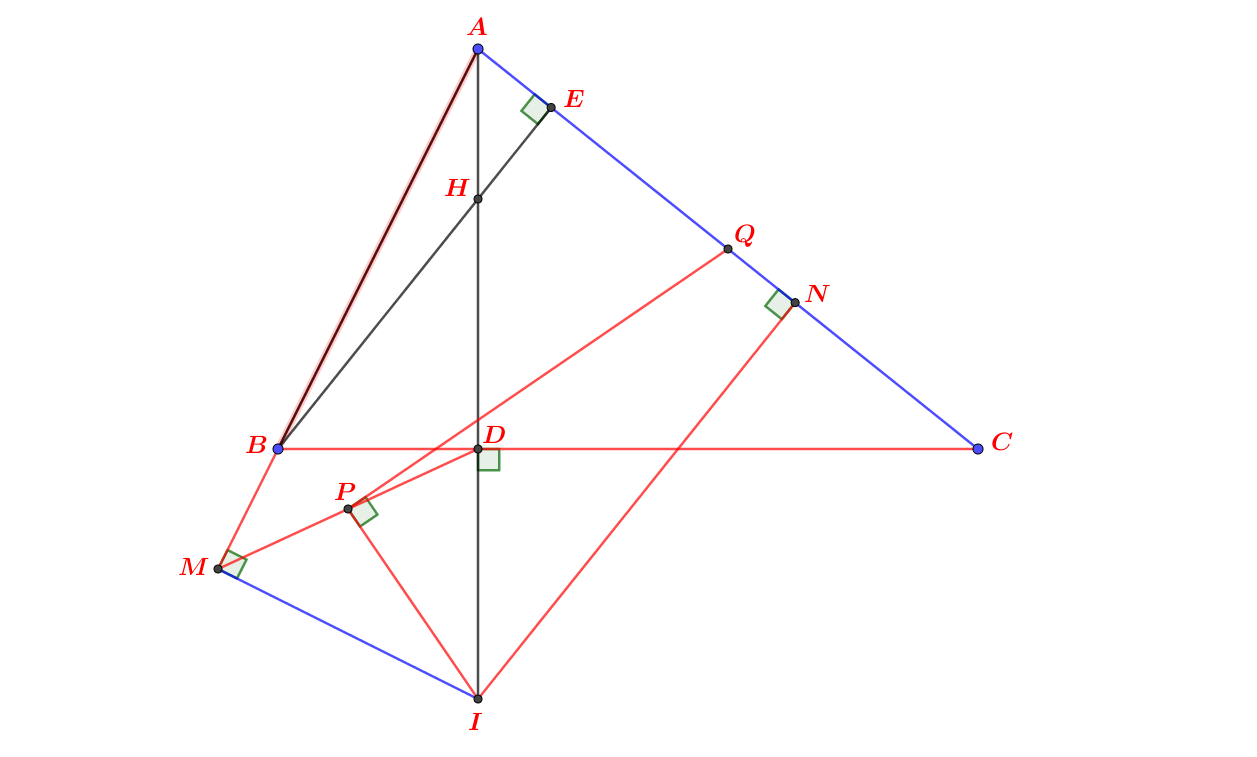
a , b tự lm nha ( dễ mà )
c) Do II đối xứng với HH qua BC⇒IH⊥BCBC⇒IH⊥BC mà HD⊥BC,D∈BC
⇒I⇒I đối xứng với HH qua D⇒DD⇒D là trung điểm của HIHI
Và MM là trung điểm của HKHK
⇒DM⇒DM là đường trung bình ΔHIKΔHIK
⇒DM∥IK⇒DM∥IK
⇒BC∥IK⇒BC∥IK
⇒BCKI⇒BCKI là hình thang
ΔCHIΔCHI có CDCD vừa là đường cao vừa là đường trung tuyến
⇒ΔCHI⇒ΔCHI cân đỉnh CC
⇒CI=CH⇒CI=CH (*)
Mà tứ giác BHCKBHCK là hình bình hành ⇒CH=BK⇒CH=BK (**)
Từ (*) và (**) suy ra CI=BKCI=BK
Tứ giác BCKIBCKI là hình bình hành có 2 đường chéo CI=BKCI=BK
Suy ra BCIKBCIK là hình thang cân.
Tứ giác HGKCHGKC có GK∥HCGK∥HC (do BHCKBHCK là hình bình hành)
⇒HGKC⇒HGKC là hình thang có đáy là GK∥HCGK∥HC
...
:< chép luôn hình cho nó thanh niên :)))