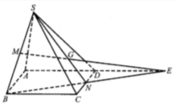
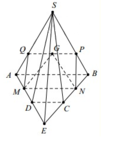
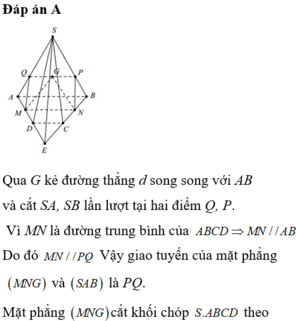
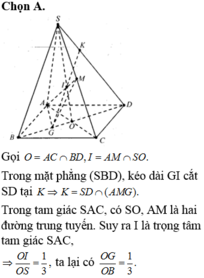
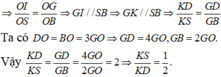1. Cho hình chóp S.ABCD có đáy là một hình bình hành. Gọi G là trọng tâm tam giác SAC. M là một điểm thay đổi trong miền hình bình hành ABCD. Tia MG cắt mặt bên của hình chóp tại điểm N đặt \(Q=\frac{MG}{NG}+\frac{NG}{MG}\)
a, tìm tất cả các vị trí của điểm M sao cho Q đạt giá trị nhỏ nhất
b, tìm giá trị lớn nhất của Q
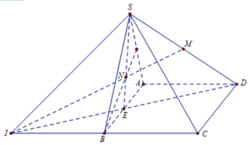
2. Cho tứ diện ABCD có hai cạnh đối bằng b,c và các cạnh còn lại bằng a. Tìm giá trị nhỏ nhất của tổng khoảng cách từ một điểm tùy ý trong không gian đến các đỉnh của tứ diện