Cho nửa đường tròn (0;R) , đường kính AD cố định. Vẽ tứ giác ABCD nôi tiếp nửa đường tròn. Gọi I là giao điểm của AC và BD, K là hình chiếu của I trên AD.
a) Chứng minh I là tâm đường tròn nội tiếp tam giác BCK
b) Gọi F là giao của CK và BD. Chứng minh \(BI.DF=BD.IF\)
C) Gọi E là trung điểm của ID. Chứng minh \(ED^2=EB.EF\)



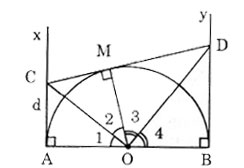 a) Ax ⊥ OA tại A, By ⊥ OB tại B nên Ax, By là các tiếp tuyến của đường tròn.
a) Ax ⊥ OA tại A, By ⊥ OB tại B nên Ax, By là các tiếp tuyến của đường tròn.


