Cho tam giác ABC cân tại A. Hãy so sánh AB và BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
5
3 tháng 3 2018
Vì tam giác ABC cân tại A có góc A bằng 61 độ nên :
\(\widehat{ABC}=\widehat{ACB}=\frac{180^o-61^o}{2}=59,5^o\)
Ta thấy góc A bằng 61 độ và góc C bằng 59,5 độ nên góc A > góc C
Do đó BC > AB ( cạnh đối diện với góc lớn hơn thì lớn hơn )
Vậy BC > AB
LB
1
20 tháng 2 2022
Bài 1:
AC=4cm
Xét ΔABC có AB<AC
nên \(\widehat{C}< \widehat{B}\)
Bài 2:
BC=6cm
=>AB+AC=14cm
mà AB=AC
nên AB=AC=7cm
Xét ΔABC có AB=AC>BC
nên \(\widehat{B}=\widehat{C}>\widehat{A}\)
PT
2
P
25 tháng 2 2022
_Xét △ABC ta có:
\(\widehat{A}\) + \(\widehat{B}\) + \(\widehat{C}\) = 180o
=> 50o + \(\widehat{B}\) + \(\widehat{C}\) = 180o
=> \(\widehat{B}\) + \(\widehat{C}\) = 180o \(-\) 50o
=> \(\widehat{B}\) + \(\widehat{C}\) = 130o : 2 = 65o
=> \(\widehat{B}\) = \(\widehat{C}\) = 65o
=> \(\widehat{A}\) < \(\widehat{B}\) => BC < AB
Vậy trong △ABC có:
BC < AB
10 tháng 4 2022
Xét ΔDBH vuông tại D và ΔECH vuông tại E có
BH=CH
\(\widehat{B}=\widehat{C}\)
Do đó: ΔDBH=ΔECH
Suy ra: HD=HE
mà HE<HC
nên HD<HC
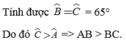
tùy trường hợp thôi