
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
AC=4cm
Xét ΔABC có AB<AC
nên \(\widehat{C}< \widehat{B}\)
Bài 2:
BC=6cm
=>AB+AC=14cm
mà AB=AC
nên AB=AC=7cm
Xét ΔABC có AB=AC>BC
nên \(\widehat{B}=\widehat{C}>\widehat{A}\)

Bài 1:
Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
mà AB>AC
nên BD>CD

Xét ΔDBH vuông tại D và ΔECH vuông tại E có
BH=CH
\(\widehat{B}=\widehat{C}\)
Do đó: ΔDBH=ΔECH
Suy ra: HD=HE
mà HE<HC
nên HD<HC

a) Ez bạn tự làm nha, mình làm sơ sơ cũng 3-4 cách rồi.:)
b) Tam giác ABC cân tại A có đường p/g góc A xuất phát từ đỉnh đồng thời là đường trung trực nên \(AD\perp BC\). và BD = CD = BC/2
Xét tam giác ABD vuông tại D (chứng minh trên), theo định lí Pythagoras:
\(AB^2=BD^2+DA^2\Leftrightarrow10^2=\frac{BC^2}{4}+DA^2\)
\(=36+DA^2\Rightarrow AD=8\) (cm) (khúc này có tính nhầm gì thì tự sửa lại nha!)
Theo đề bài ta có AB = AC = 10 < BC = 12
Hay AC < BC. Theo quan hệ giữa góc và cạnh đối diện trong tam giác ABC ta có \(\widehat{ABC}< \widehat{BAC}\) (Cái khúc này không chắc, sai thì thôi)
c) Hướng dẫn:
\(\Delta\)EDB = \(\Delta\)FDC (cạnh huyền - góc nhọn)
Suy ra EB = FC. Từ đó suy ra AE = AF.
Suy ra tam giác AEF cân tại A suy ra \(\widehat{AEF}=\frac{180^o-\widehat{A}}{2}\) (1)
Mặt khác tam giác ABC cân tại A nên \(\widehat{ABC}=\frac{180^o-\widehat{A}}{2}\) (2)
Từ (1) và (2) suy ra đpcm

_Xét △ABC ta có:
\(\widehat{A}\) + \(\widehat{B}\) + \(\widehat{C}\) = 180o
=> 50o + \(\widehat{B}\) + \(\widehat{C}\) = 180o
=> \(\widehat{B}\) + \(\widehat{C}\) = 180o \(-\) 50o
=> \(\widehat{B}\) + \(\widehat{C}\) = 130o : 2 = 65o
=> \(\widehat{B}\) = \(\widehat{C}\) = 65o
=> \(\widehat{A}\) < \(\widehat{B}\) => BC < AB
Vậy trong △ABC có:
BC < AB
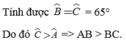
Vì tam giác ABC cân tại A có góc A bằng 61 độ nên :
\(\widehat{ABC}=\widehat{ACB}=\frac{180^o-61^o}{2}=59,5^o\)
Ta thấy góc A bằng 61 độ và góc C bằng 59,5 độ nên góc A > góc C
Do đó BC > AB ( cạnh đối diện với góc lớn hơn thì lớn hơn )
Vậy BC > AB
AB < BC