Mọi người giúp em giải bài VD với ạ em cảm ơn nhiều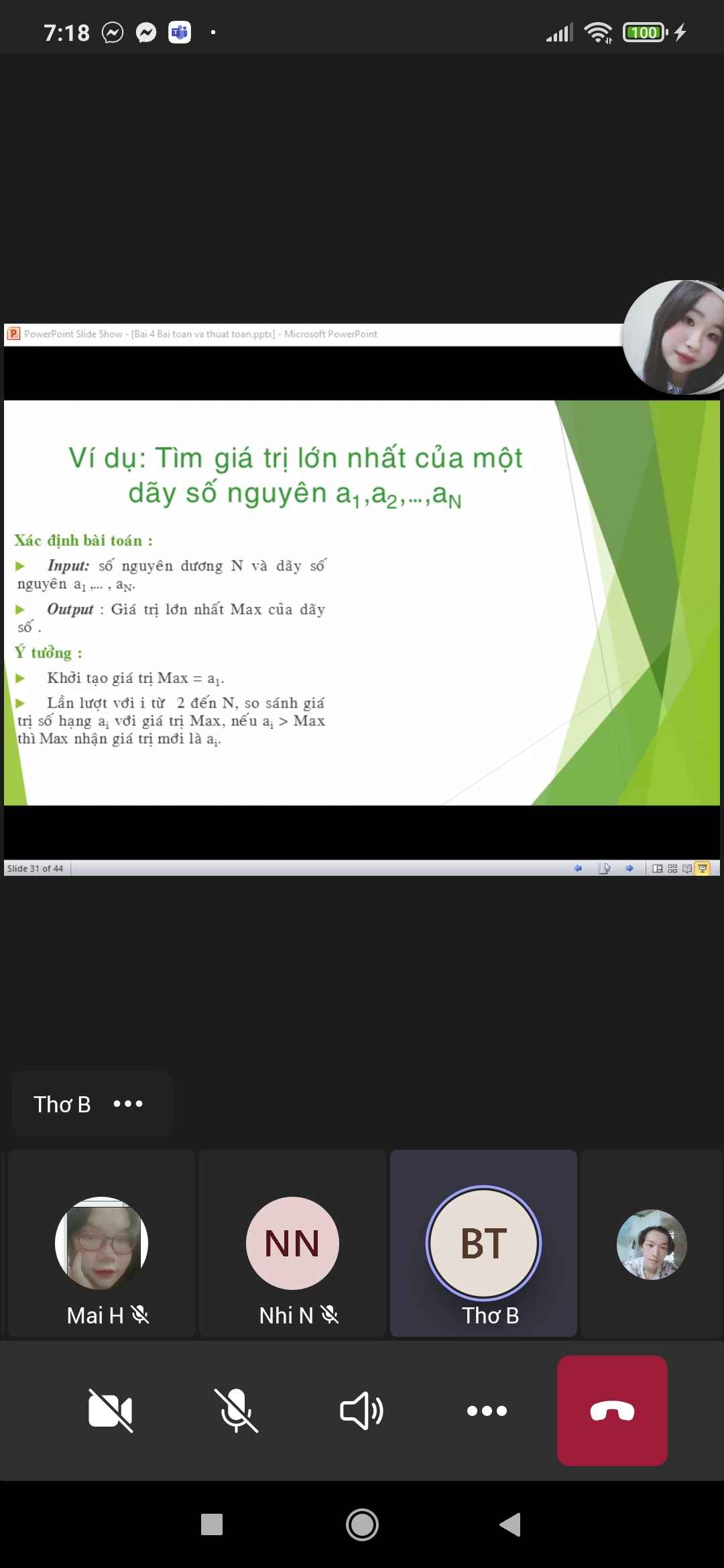
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TD
2
Q
19 tháng 5 2021
vẽ lại mạch ta có RAM//RMN//RNB
đặt theo thứ tự 3 R là a,b,c
ta có a+b+c=1 (1)
điện trở tương đương \(\dfrac{1}{R_{td}}=\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\) \(\Rightarrow I=\dfrac{U}{R_{td}}=9.\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\) với a,b,c>0
áp dụng bất đẳng thức cô si cho \(\dfrac{1}{a},\dfrac{1}{b},\dfrac{1}{c}\) \(\Rightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{3}{\sqrt[3]{abc}}\ge\dfrac{3}{\left(\dfrac{a+b+c}{3}\right)}=\dfrac{9}{a+b+c}=9\)
\(\Leftrightarrow9\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\ge81\Leftrightarrow I\ge81\) I min =81 ( úi dồi ôi O_o hơi to mà vẫn đúng đá nhỉ)
dấu ''='' xảy ra \(\Leftrightarrow a=b=c\left(2\right)\)
từ (1) (2) \(\Rightarrow a=b=c=\dfrac{1}{3}\left(\Omega\right)\)
vậy ... (V LUN MẤT CẢ BUỔI TỐI R BÀI KHÓ QUÁ EM ĐANG ÔN HSG À )
TN
1
13 tháng 6 2023
a: góc AED+góc AFD=180 độ
=>AEDF nội tiếp
=>góc AEF=góc ADF=góc C
=>góc FEB+góc FCB=180 độ
=>FEBC nội tiếp
b: Xét ΔGBE và ΔGFC có
góc GBE=góc GFC
góc G chung
=>ΔGBE đồng dạng với ΔGFC
=>GB/GF=GE/GC
=>GB*GC=GF*GE
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 7 2021
\(A=\dfrac{\sqrt{20}-6}{\sqrt{14-6\sqrt{5}}}-\dfrac{\sqrt{20}-\sqrt{28}}{\sqrt{12-2\sqrt{35}}}=\dfrac{-2\left(3-\sqrt{5}\right)}{\sqrt{\left(3-\sqrt{5}\right)^2}}+\dfrac{2\left(\sqrt{7}-\sqrt{5}\right)}{\sqrt{\left(\sqrt{7}-\sqrt{5}\right)^2}}\)
\(=\dfrac{-2\left(3-\sqrt{5}\right)}{3-\sqrt{5}}+\dfrac{2\left(\sqrt{7}-\sqrt{5}\right)}{\sqrt{7}-\sqrt{5}}=-2+2=0\)
\(B=\sqrt{\dfrac{\left(9-4\sqrt{3}\right)\left(6-\sqrt{3}\right)}{\left(6-\sqrt{3}\right)\left(6+\sqrt{3}\right)}}-\sqrt{\dfrac{\left(3+4\sqrt{3}\right)\left(5\sqrt{3}+6\right)}{\left(5\sqrt{3}-6\right)\left(5\sqrt{3}+6\right)}}\)
\(=\sqrt{\dfrac{66-33\sqrt{3}}{33}}-\sqrt{\dfrac{78+39\sqrt{3}}{39}}=\sqrt{2-\sqrt{3}}-\sqrt{2+\sqrt{3}}\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{4-2\sqrt{3}}-\sqrt{4+2\sqrt{3}}\right)=\dfrac{1}{\sqrt{2}}\left(\sqrt{\left(\sqrt{3}-1\right)^2}-\sqrt{\left(\sqrt{3}+1\right)^2}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{3}-1-\sqrt{3}-1\right)=-\sqrt{2}\)
28 tháng 7 2021
a) Ta có: \(A=\dfrac{\sqrt{10}-3\sqrt{2}}{\sqrt{7-3\sqrt{5}}}-\dfrac{\sqrt{10}-\sqrt{14}}{\sqrt{6-\sqrt{35}}}\)
\(=\dfrac{2\sqrt{5}-6}{3-\sqrt{5}}-\dfrac{2\sqrt{5}-2\sqrt{7}}{\sqrt{7}-\sqrt{5}}\)
\(=\dfrac{\left(2\sqrt{5}-6\right)\left(3+\sqrt{5}\right)}{4}-\dfrac{\left(2\sqrt{5}-2\sqrt{7}\right)\left(\sqrt{7}+\sqrt{5}\right)}{2}\)
\(=\dfrac{\left(\sqrt{5}-3\right)\left(3+\sqrt{5}\right)-\left(2\sqrt{5}-2\sqrt{7}\right)\left(\sqrt{7}+\sqrt{5}\right)}{2}\)
\(=\dfrac{5-9-2\left(5-7\right)}{2}\)
\(=\dfrac{-4-2\cdot\left(-2\right)}{2}\)
\(=0\)
J
1
5 tháng 12 2023
Câu 10:
a: ĐKXĐ: \(\left\{{}\begin{matrix}x\notin\left\{2;-1\right\}\\y\ne-5\end{matrix}\right.\)
\(A=\dfrac{y+5}{x^2-4x+4}\cdot\dfrac{x^2-4}{x+1}\cdot\dfrac{x-2}{y+5}\)
\(=\dfrac{y+5}{y+5}\cdot\dfrac{\left(x^2-4\right)}{x^2-4x+4}\cdot\dfrac{x-2}{x+1}\)
\(=\dfrac{\left(x^2-4\right)\cdot\left(x-2\right)}{\left(x+1\right)\left(x^2-4x+4\right)}\)
\(=\dfrac{\left(x+2\right)\left(x-2\right)\cdot\left(x-2\right)}{\left(x+1\right)\left(x-2\right)^2}=\dfrac{x+2}{x+1}\)
b: \(A=\dfrac{x+2}{x+1}\)
=>A không phụ thuộc vào biến y
Khi x=1/2 thì \(A=\left(\dfrac{1}{2}+2\right):\left(\dfrac{1}{2}+1\right)=\dfrac{5}{2}:\dfrac{3}{2}=\dfrac{5}{2}\cdot\dfrac{2}{3}=\dfrac{5}{3}\)
Câu 12:
a: \(A=\dfrac{x}{x+3}+\dfrac{2x}{x-3}+\dfrac{9-3x^2}{x^2-9}\)
\(=\dfrac{x}{x+3}+\dfrac{2x}{x-3}+\dfrac{9-3x^2}{\left(x+3\right)\left(x-3\right)}\)
\(=\dfrac{x\left(x-3\right)+2x\left(x+3\right)+9-3x^2}{\left(x+3\right)\left(x-3\right)}\)
\(=\dfrac{x^2-3x+2x^2+6x+9-3x^2}{\left(x+3\right)\left(x-3\right)}\)
\(=\dfrac{3x+9}{\left(x+3\right)\left(x-3\right)}=\dfrac{3\left(x+3\right)}{\left(x+3\right)\left(x-3\right)}=\dfrac{3}{x-3}\)
b: Khi x=1 thì \(A=\dfrac{3}{1-3}=\dfrac{3}{-2}=-\dfrac{3}{2}\)
\(x+\dfrac{1}{3}=\dfrac{10}{3}\)
=>\(x=\dfrac{10}{3}-\dfrac{1}{3}\)
=>\(x=\dfrac{9}{3}=3\left(loại\right)\)
Vậy: Khi x=3 thì A không có giá trị
c: \(B=A\cdot\dfrac{x-3}{x^2-4x+5}\)
\(=\dfrac{3}{x-3}\cdot\dfrac{x-3}{x^2-4x+5}\)
\(=\dfrac{3}{x^2-4x+5}\)
\(x^2-4x+5=x^2-4x+4+1=\left(x-2\right)^2+1>=1\forall x\) thỏa mãn ĐKXĐ
=>\(B=\dfrac{3}{x^2-4x+5}< =\dfrac{3}{1}=3\forall x\) thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi x-2=0
=>x=2
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 8 2021
Do MN là đường trung bình tam giác ABC \(\Rightarrow MN||AB\) mà \(AB||CD\Rightarrow MN||CD\)
MN và (ABCD) không có điểm chung \(\Rightarrow MN||\left(ABCD\right)\)
MN và (SCD) không có điểm chung \(\Rightarrow MN||\left(SCD\right)\)
MN nằm trên (SAB) nên MN không song song (SAB)
Vậy MN song song với cả (ABCD) và (SCD)
HK
1
12 tháng 12 2021
Đề 1:
Bài 1:
\(a,=\sqrt{\left(\sqrt{7}+1\right)^2}-\left|-1+\sqrt{7}\right|=\sqrt{7}+1-\sqrt{7}+1=2\\ b,=2\sqrt{2}-4\sqrt{2}-5\sqrt{2}+\dfrac{\sqrt{2}}{2}=\dfrac{\sqrt{2}}{2}-7\sqrt{2}=\dfrac{-13\sqrt{2}}{\sqrt{2}}\)
Bài 2:
\(PT\Leftrightarrow\sqrt{\left(x-\dfrac{1}{2}\right)^2}=\dfrac{1}{2}\Leftrightarrow\left|x-\dfrac{1}{2}\right|=\dfrac{1}{2}\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}+\dfrac{1}{2}=1\\x=-\dfrac{1}{2}+\dfrac{1}{2}=0\end{matrix}\right.\)
Bài 3:
\(a,M=\dfrac{a-2\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{2\sqrt{a}}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}=\dfrac{2\left(\sqrt{a}-1\right)^2}{\left(\sqrt{a}-1\right)^2\left(\sqrt{a}+1\right)}=\dfrac{2}{\sqrt{a}+1}\\ b,M< 1\Leftrightarrow\dfrac{2}{\sqrt{a}+1}-1< 0\Leftrightarrow\dfrac{1-\sqrt{a}}{\sqrt{a}+1}< 0\\ \Leftrightarrow1-\sqrt{a}< 0\left(\sqrt{a}+1>0\right)\\ \Leftrightarrow a>1\)
1 tháng 7 2023
8.31:
a: Xét ΔABD có AM/AB=AQ/AD
nên MQ//BD và MQ=BD/2
Xét ΔCBD có CN/CB=CP/CD
nên NP//BD và NP=BD/2
=>MQ//NP và MQ=NP
XétΔBAC có BM/BA=BN/BC
nên MN//AC
=>MN vuông góc BD
=>MN vuông góc MQ
Xét tứ giác MNPQ có
MQ//NP
MQ=NP
góc NMQ=90 độ
=>MNPQ là hình chữ nhật
=>M,N,P,Q cùng nằm trên 1 đường tròn
#include <bits/stdc++.h>
using namespace std;
long long x,n,i,max;
int main()
{
cin>>n;
cin>>x;
max=x;
for (i=1; i<n; i++)
{
cin>>x;
if (max<=x) max=x;
}
cout<<max;
return 0;
}
Bước 1: Nhập N và dãy số a1,..., aN
Bước 2: Max ← a1, i ← 2
Bước 3: Nếu i > N thì thông báo giá trị lớn nhất và kết thúc thuật toán.
Bước 4:
4.1. Nếu Max < ai thì Max ← ai
4.2. i ← i + 1 và quay lại bước 3.