Cho tam giác ABC vuông tại A có AB< AC, điểm D thuộc cạnh AC. Gọi E, F, G theo thứ tự là trung điểm của BD, BC, DC. Kết quả so sánh giữa độ dài hai đoạn thẳng AF và EG là AF...EG.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 4 2017
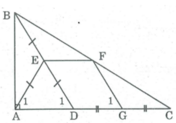
* Trong ∆ BDC, ta có:
E là trung điểm của BD (gt)
F là trung điểm của BC (gt)
Suy ra EF là đường trung bình của tam giác BCD
⇒ EF // DC hay EF // AG
Suy ra tứ giác AEFG là hình thang
G là trung điểm của DC (gt)
Nên FG là đường trung bình của tam giác BCD
⇒ FG // BD ⇒ ∠ G 1 = ∠ D 1 (đồng vị) (1)
* Trong tam giác ABD vuông tại A có AE là đường trung tuyến ứng với cạnh huyền BD
⇒ AE = ED = 1/2 BD (tính chất tam giác vuông)
Suy ra: tam giác AED cân tại E nên ∠ A 1 = ∠ D 1 (2)
Từ (1) và (2) suy ra: ∠ A 1 = ∠ G 1
Vậy hình thang AEFG là hình thang cân.
21 tháng 3 2023
a: Xét ΔABD và ΔAED có
AB=AE
góc BAD=góc EAD
AD chung
=>ΔABD=ΔAED
b: ΔABD=ΔAED
=>góc AED=góc ABD=90 độ
c: Xét ΔAEF vuông tại A và ΔABC vuông tại B có
AE=AB
góc EAF chung
=>ΔAEF=ΔABC
=>AF=AC
d: DB=DE
mà DE<DC
nên DB<DC
21 tháng 6 2022
Câu 3:
Xét ΔMDC có AB//CD
nên MA/MD=MB/MC(1)
Xét ΔMDK có AI//DK
nên AI/DK=MA/MD(2)
Xét ΔMKC có IB//KC
nên IB/KC=MB/MC(3)
Từ (1), (2) và (3) suy ra AI/DK=IB/KC=MI/MK
Vì AI//KC nên AI/KC=NI/NK=NA/NC
Vì IB//DK nên IB/DK=NI/NK
=>AI/KC=IB/DK
mà AI/DK=IB/KC
nên \(\dfrac{AI}{KC}\cdot\dfrac{AI}{DK}=\dfrac{IB}{DK}\cdot\dfrac{IB}{DC}\)
=>AI=IB
=>I là trung điểm của AB
AI/DK=BI/KC
mà AI=BI
nên DK=KC
hay K là trung điểm của CD