Làm dễ hiểu giúp em với ạ
K
Khách
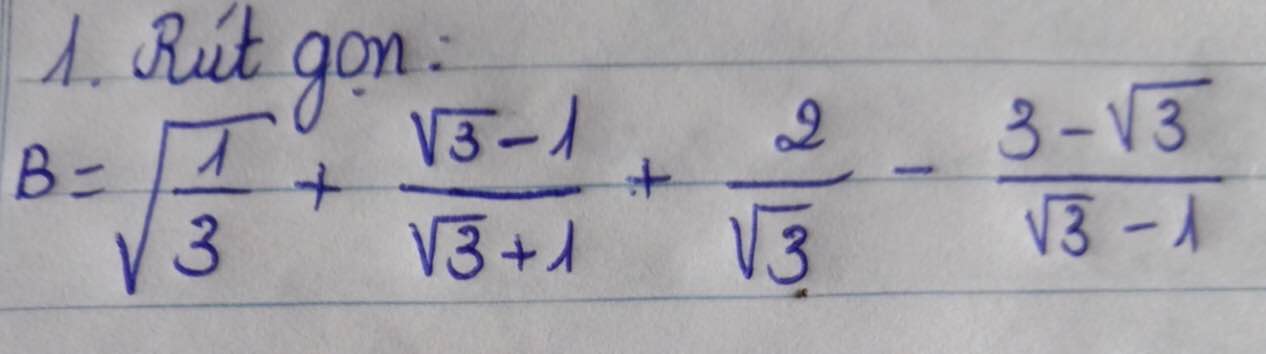
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TT
2
3 tháng 11 2021
\(a,ĐK:-3x\ge0\Leftrightarrow x\le0\left(-3< 0\right)\\ b,ĐK:4-2x\ge0\Leftrightarrow-2x\ge-4\Leftrightarrow x\le2\\ c,ĐK:\dfrac{1}{2x-5}\ge0\Leftrightarrow2x-5>0\left(1>0;2x-5\ne0\right)\\ \Leftrightarrow x>\dfrac{5}{2}\\ d,ĐK:\dfrac{4x+7}{-3}\ge0\Leftrightarrow4x+7\le0\left(-3< 0\right)\Leftrightarrow x\le-\dfrac{7}{4}\)
HT
1
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2021
\(B_2=\left\{x;x=2k,k\in N\right\}\)
\(B_4=\left\{x;x=4m,m\in N\right\}\)
Do \(4m=2.\left(2m\right)\Rightarrow B_4\subset B_2\)
\(\Rightarrow B_2\cap B_4=B_4\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 11 2021
11c.
Từ đề bài ta có:
\(\left\{{}\begin{matrix}\dfrac{16a-b^2}{4a}=\dfrac{9}{2}\\16a+4b+4=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2b^2=-4a\\b=-4a-1\end{matrix}\right.\)
\(\Rightarrow2b^2-b=1\Leftrightarrow2b^2-b-1=0\Rightarrow\left[{}\begin{matrix}b=1\Rightarrow a=-\dfrac{1}{2}\\b=-\dfrac{1}{2}\Rightarrow a=-\dfrac{1}{8}\end{matrix}\right.\)
Có 2 parabol thỏa mãn: \(\left[{}\begin{matrix}y=-\dfrac{1}{2}x^2+x+4\\y=-\dfrac{1}{8}x^2-\dfrac{1}{2}x+4\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 11 2021
4f.
Từ đề bài ta có:
\(\left\{{}\begin{matrix}1+b+c=0\\\dfrac{4c-b^2}{4}=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}c=-b-1\\c=\dfrac{b^2}{4}-1\end{matrix}\right.\)
\(\Rightarrow\dfrac{b^2}{4}+b=0\)
\(\Rightarrow\left[{}\begin{matrix}b=0\Rightarrow c=-1\\b=-4\Rightarrow c=3\end{matrix}\right.\)
Có 2 parabol thỏa mãn: \(\left[{}\begin{matrix}y=x^2-1\\y=x^2-4x+3\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 4 2022
\(y'=\left(x^3\right)'-\left(4x^2\right)'+\left(1\right)'=3x^2-8x\)
Hệ số góc của tiếp tuyến tại điểm có hoành độ bằng 1 là \(y'\left(1\right)\)
\(y'\left(1\right)=3.1^2-8.1=-5\)
30 tháng 7 2018
Tìm nghiệm nguyên dương của phương trình: x^2+(x+y)^2=(x+9)^2 - Đại số - Diễn đàn Toán học
7 tháng 9 2021
\(\left(a-\dfrac{a^2+b^2}{a+b}\right)\left(\dfrac{1}{b}+\dfrac{2}{a-b}\right)\)
\(=\dfrac{a^2+ab-a^2-b^2}{a+b}\cdot\dfrac{a-b+2b}{b\left(a-b\right)}\)
\(=\dfrac{b\left(a-b\right)}{a+b}\cdot\dfrac{a+b}{b\left(a-b\right)}\)
=1
7 tháng 9 2021
\(\left(a-\dfrac{x^2+a^2}{x+a}\right)\left(\dfrac{2a}{x}-\dfrac{4a}{x-a}\right)\)
\(=\dfrac{ax+a^2-x^2-a^2}{x+a}\cdot\dfrac{2ax-2a^2-4ax}{x\left(x-a\right)}\)
\(=\dfrac{a\left(x-a\right)}{x+a}\cdot\dfrac{-2a^2-2ax}{x\left(x-a\right)}\)
\(=\dfrac{a}{x+a}\cdot\dfrac{-2a\left(a+x\right)}{x}\)
\(=\dfrac{-2a^2}{x}\)
HP
7 tháng 9 2021
\(\left(a-\dfrac{x^2+a^2}{x+a}\right)\left(\dfrac{2a}{x}-\dfrac{4a}{x-a}\right)\)
\(=\dfrac{ax+a^2-x^2-a^2}{x+a}.\dfrac{2a\left(x-a\right)-4ax}{x\left(x-a\right)}\)
\(=\dfrac{x\left(a-x\right)}{x+a}.\dfrac{-2a^2-2ax}{x\left(x-a\right)}\)
\(=\dfrac{x\left(a-x\right)}{x+a}.\dfrac{-2a\left(a+x\right)}{x\left(x-a\right)}\)
\(=2a\)
\(B=\sqrt{\dfrac{1}{3}}+\dfrac{\sqrt{3}-1}{\sqrt{3}+1}+\dfrac{2}{\sqrt{3}}-\dfrac{3-\sqrt{3}}{\sqrt{3}-1}\)
\(\Rightarrow B=\dfrac{\sqrt{1}}{\sqrt{3}}+\dfrac{\left(\sqrt{3}-1\right)^2}{\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)}+\dfrac{2}{\sqrt{3}}-\dfrac{\sqrt{3}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}\)
\(\Rightarrow B=\left(\dfrac{1}{\sqrt{3}}+\dfrac{2}{\sqrt{3}}\right)+\dfrac{3-2\sqrt{3}+1}{\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)}-\sqrt{3}\)
\(\Rightarrow B=\dfrac{3}{\sqrt{3}}+\dfrac{4-2\sqrt{3}}{\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)}-\sqrt{3}\)
\(\Rightarrow B=\sqrt{3}+\dfrac{4-2\sqrt{3}}{\sqrt{3^2}-1^2}-\sqrt{3}\)
\(\Rightarrow B=\dfrac{4-2\sqrt{3}}{2}\)
\(\Rightarrow B=2-\sqrt{3}\)
⇔ \(B=\dfrac{1}{\sqrt{3}}+\dfrac{\left(\sqrt{3}-1\right)\left(\sqrt{3}-1\right)}{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}+\dfrac{2}{\sqrt{3}}-\dfrac{\sqrt{3}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}\)
⇔ \(B=\dfrac{\text{3}}{\sqrt{3}}+\dfrac{3-2\sqrt{3}+1}{3-1}-\sqrt{3}\)
⇔ \(B=\sqrt{3}+\dfrac{\text{4}-2\sqrt{3}}{\text{2}}-\sqrt{3}\)
⇔ \(B=\dfrac{2\left(2-\sqrt{3}\right)}{2}=2-\sqrt{3}\)