
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,ĐK:-3x\ge0\Leftrightarrow x\le0\left(-3< 0\right)\\ b,ĐK:4-2x\ge0\Leftrightarrow-2x\ge-4\Leftrightarrow x\le2\\ c,ĐK:\dfrac{1}{2x-5}\ge0\Leftrightarrow2x-5>0\left(1>0;2x-5\ne0\right)\\ \Leftrightarrow x>\dfrac{5}{2}\\ d,ĐK:\dfrac{4x+7}{-3}\ge0\Leftrightarrow4x+7\le0\left(-3< 0\right)\Leftrightarrow x\le-\dfrac{7}{4}\)

Tìm nghiệm nguyên dương của phương trình: x^2+(x+y)^2=(x+9)^2 - Đại số - Diễn đàn Toán học

a.
\(2x-x^2+7=-\left(x^2-2x+1\right)+8=-\left(x-1\right)^2+8\le8\)
\(\Rightarrow2+\sqrt{2x-x^2+7}\le2+\sqrt{8}=2+2\sqrt{2}\)
\(\Rightarrow\dfrac{3}{2+\sqrt{2x-x^2+7}}\ge\dfrac{3}{2+2\sqrt{2}}=\dfrac{3\sqrt{2}-3}{2}\)
\(A_{min}=\dfrac{3\sqrt{2}-3}{2}\) khi \(x=1\)
b. ĐKXĐ: \(x\le1\)
\(B=-\left(1-x-\sqrt{2\left(1-x\right)}+\dfrac{1}{2}-\dfrac{1}{2}-1\right)\)
\(B=-\left(1-x-\sqrt{2\left(1-x\right)}+\dfrac{1}{2}\right)+\dfrac{3}{2}\)
\(B=-\left(\sqrt{1-x}-\dfrac{\sqrt{2}}{2}\right)^2+\dfrac{3}{2}\le\dfrac{3}{2}\)
\(B_{max}=\dfrac{3}{2}\) khi\(x=\dfrac{1}{2}\)


`(4\sqrt{6}+x)^2=8^2+(6+\sqrt{x^2+4})^2`
`<=>96+8\sqrt{6}x+x^2=64+36+12\sqrt{x^2+4}+x^2+4`
`<=>2\sqrt{6}x-2=3\sqrt{x^2+4}` `ĐK: x >= \sqrt{6}/6`
`<=>24x^2-8\sqrt{6}x+4=9x^2+36`
`<=>15x^2-8\sqrt{6}x-32=0`
`<=>x^2-[8\sqrt{6}]/15x-32/15=0`
`<=>(x-[4\sqrt{6}]/15)^2-64/25=0`
`<=>|x-[4\sqrt{6}]/15|=8/5`
`<=>[(x=[24+4\sqrt{6}]/15 (t//m)),(x=[-24+4\sqrt{6}]/15(ko t//m)):}`

a: \(\sqrt{252}+\dfrac{1}{3}\sqrt{63}-\sqrt{175}\)
\(=4\sqrt{7}+\sqrt{7}-5\sqrt{7}\)
=0

\(=\sqrt{5\sqrt{3}+\sqrt{5\sqrt{48-10\sqrt{\left(2+\sqrt{3}\right)^2}}}}\)
\(=\sqrt{5\sqrt{3}+\sqrt{5\sqrt{48-10\left(2+\sqrt{3}\right)}}}\)
\(=\sqrt{5\sqrt{3}+\sqrt{5\sqrt{48-20-10\sqrt{3}}}}\)
\(=\sqrt{5\sqrt{3}+\sqrt{5\sqrt{28-10\sqrt{3}}}}\)
\(=\sqrt{5\sqrt{3}+\sqrt{5\sqrt{\left(5-\sqrt{3}\right)^2}}}\)
\(=\sqrt{5\sqrt{3}+\sqrt{5\left(5-\sqrt{3}\right)}}=\sqrt{5\sqrt{3}+\sqrt{25-5\sqrt{3}}}\)
Trần Đức Thắng lm nốt đi

1.
Xét pt đầu:
\(x^2-xy+x-y=0\)
\(\Leftrightarrow x\left(x-y\right)+x-y=0\)
\(\Leftrightarrow\left(x+1\right)\left(x-y\right)=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=y\end{matrix}\right.\)
TH1: \(x=-1\) thay xuống pt dươi:
\(\sqrt{y^2+15}=-3-2+\sqrt{9}\Leftrightarrow\sqrt{y^2+15}=-2< 0\) (vô nghiệm)
TH2: thay \(y=x\) xuống pt dưới:
\(\sqrt{x^2+15}=3x-2+\sqrt{x^2+8}\) (1)
\(\Rightarrow3x-2=\sqrt{x^2+15}-\sqrt{x^2+8}=\dfrac{7}{\sqrt{x^2+15}+\sqrt{x^2+8}}>0\)
\(\Rightarrow x>\dfrac{2}{3}\)
Do đó (1) tương đương:
\(3x-2+\sqrt{x^2+8}-\sqrt{x^2+15}=0\)
\(\Leftrightarrow3x-3+\sqrt{x^2+8}-3+4-\sqrt{x^2+15}=0\)
\(\Leftrightarrow3\left(x-1\right)+\dfrac{\left(x-1\right)\left(x+1\right)}{\sqrt{x^2+8}+3}-\dfrac{\left(x-1\right)\left(x+1\right)}{\sqrt{x^2+15}+4}=0\)
\(\Leftrightarrow\left(x-1\right)\left[3+\left(x+1\right)\left(\dfrac{1}{\sqrt{x^2+8}+3}-\dfrac{1}{\sqrt{x^2+15}+4}\right)\right]=0\)
\(\Leftrightarrow x-1=0\) (do \(x+1>0\) nên ngoặc phía sau luôn dương)
\(\Leftrightarrow x=y=1\)
2.
Pt đầu tương đương:
\(y^2-x+x^2-2xy+x=0\)
\(\Leftrightarrow\left(x-y\right)^2=0\Leftrightarrow y=x\)
Thay xuống pt dưới:
\(2x^2+x-x^2+x-3=0\)
\(\Leftrightarrow x^2+2x-3=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\Rightarrow y=1\\x=-3\Rightarrow y=-3\end{matrix}\right.\)
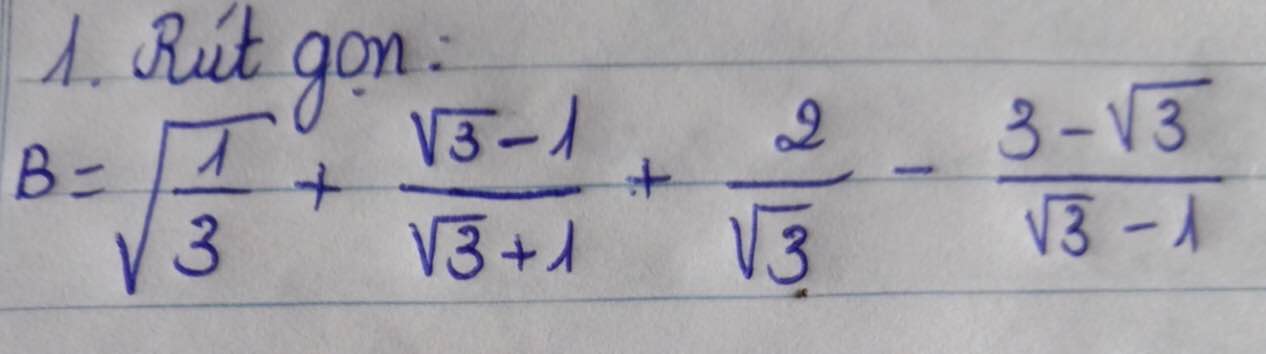


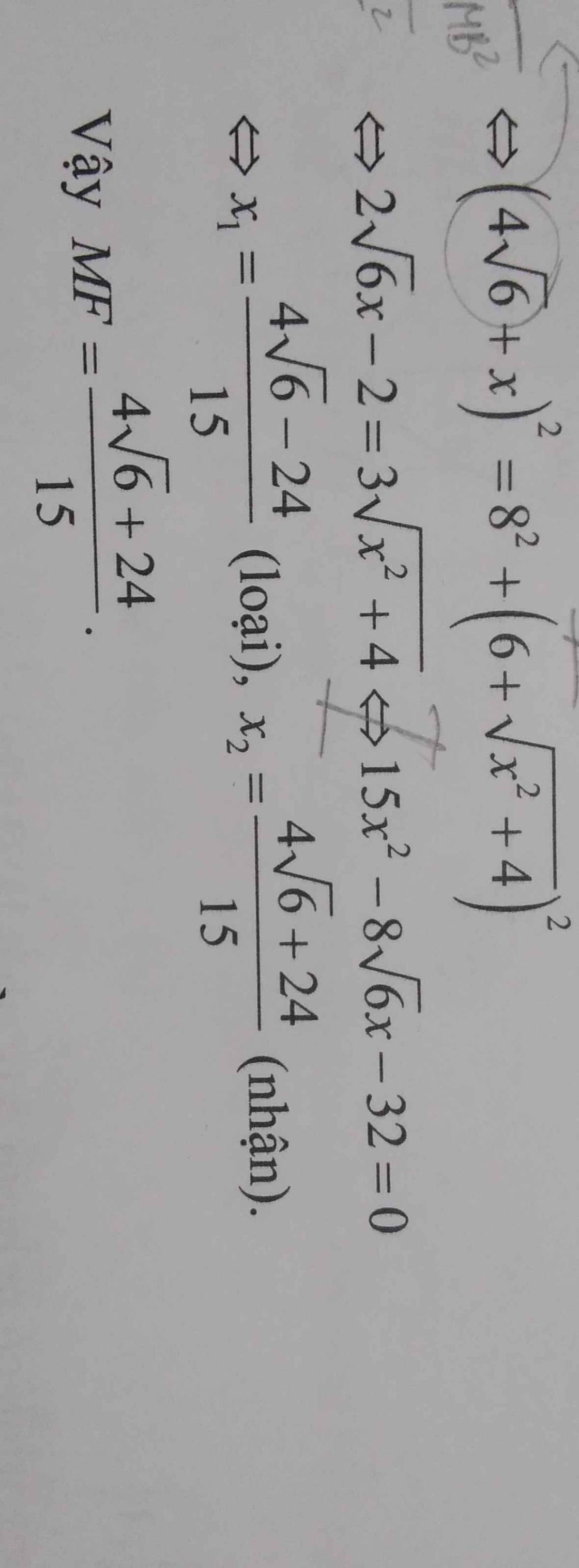


\(B=\sqrt{\dfrac{1}{3}}+\dfrac{\sqrt{3}-1}{\sqrt{3}+1}+\dfrac{2}{\sqrt{3}}-\dfrac{3-\sqrt{3}}{\sqrt{3}-1}\)
\(\Rightarrow B=\dfrac{\sqrt{1}}{\sqrt{3}}+\dfrac{\left(\sqrt{3}-1\right)^2}{\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)}+\dfrac{2}{\sqrt{3}}-\dfrac{\sqrt{3}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}\)
\(\Rightarrow B=\left(\dfrac{1}{\sqrt{3}}+\dfrac{2}{\sqrt{3}}\right)+\dfrac{3-2\sqrt{3}+1}{\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)}-\sqrt{3}\)
\(\Rightarrow B=\dfrac{3}{\sqrt{3}}+\dfrac{4-2\sqrt{3}}{\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)}-\sqrt{3}\)
\(\Rightarrow B=\sqrt{3}+\dfrac{4-2\sqrt{3}}{\sqrt{3^2}-1^2}-\sqrt{3}\)
\(\Rightarrow B=\dfrac{4-2\sqrt{3}}{2}\)
\(\Rightarrow B=2-\sqrt{3}\)
⇔ \(B=\dfrac{1}{\sqrt{3}}+\dfrac{\left(\sqrt{3}-1\right)\left(\sqrt{3}-1\right)}{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}+\dfrac{2}{\sqrt{3}}-\dfrac{\sqrt{3}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}\)
⇔ \(B=\dfrac{\text{3}}{\sqrt{3}}+\dfrac{3-2\sqrt{3}+1}{3-1}-\sqrt{3}\)
⇔ \(B=\sqrt{3}+\dfrac{\text{4}-2\sqrt{3}}{\text{2}}-\sqrt{3}\)
⇔ \(B=\dfrac{2\left(2-\sqrt{3}\right)}{2}=2-\sqrt{3}\)