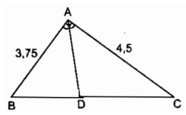
Cho \(\Delta ABC\) vuông tại A có BD là phân giác. Biết rằng AD = 1cm, \(BD=\sqrt{10}cm\) . Tính độ dài cạnh BC (viết kết quả dưới dạng số thập phân).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 8 2019
xét tam giác vuông ABD vuông tại A có:
\(AB^2=BD^2+AD^2\Rightarrow AB=\sqrt{BD^2+AD^2}=\sqrt{\left(\sqrt{10}\right)^2+1^2}=\sqrt{11}\left(cm\right)\approx3,32\)
vì BD là phân giác của tam giác vuông ABC => BD cũng là đường cao của tam giác vuông ABC.
theo hệ thức lượng trong tam giác vuông ABC có:
\(BD^2=AD.CD\Rightarrow CD=\frac{BD^2}{AD}=\frac{\left(\sqrt{10}\right)^2}{1}=10\left(cm\right)\)
theo tính chất phân giác trong tam giác ta có:
\(\frac{BA}{AD}=\frac{BC}{CD}\Rightarrow BC=\frac{BA.CD}{AD}=\frac{\sqrt{11}.10}{1}=10\sqrt{11}\left(cm\right)\approx33,17\)
= 500
AC). Tính AD, DC, BD?
3 tháng 2 2021
Áp dụng định lí Pytago vào ΔABD vuông tại A, ta được:
\(BD^2=AD^2+AB^2\)
\(\Leftrightarrow AB^2=BD^2-AD^2=\left(\sqrt{10}\right)^2-1^2=9\)
hay AB=3(cm)
Xét ΔABD vuông tại A có
\(\sin\widehat{ABD}=\dfrac{AD}{BD}=\dfrac{1}{\sqrt{10}}\)
nên \(\widehat{ABD}\simeq18^026'\)
mà \(\widehat{ABC}=2\cdot\widehat{ABD}\)(BD là tia phân giác của \(\widehat{ABC}\))
nên \(\widehat{ABC}\simeq2\cdot18^026'=36^052'\)
Xét ΔABC vuông tại A có
\(AB=BC\cdot\cos\widehat{ABC}\)
\(\Leftrightarrow BC=\dfrac{AB}{\cos\widehat{ABC}}=\dfrac{3}{\cos36^052'}\)
hay \(BC\simeq3.75cm\)
Vậy: \(BC\simeq3.75cm\)
MP
1 tháng 9 2017
\(\text{Gọi AH là hình chiếu của AB trên cạnh huyền BC.}\)
\(\text{Áp dụng hệ thức lượng vào ∆ABC vuông tại A, ta có: }\)\(AC^2=CH.BC\)
\(\Leftrightarrow CH=\frac{AC^2}{BC}=\frac{14^2}{16}=12,25\left(cm\right)\)
\(\text{Áp dụng định lý Pytago vào ∆HAC vuông tại H:}\) \(AH^2=AC^2-HC^2\)
\(\Leftrightarrow AH=\sqrt{14^2-12,25^2}=\sqrt{\frac{735}{16}}=\frac{7\sqrt{15}}{4}\left(cm\right)\)