Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng định lí Pytago vào ΔABD vuông tại A, ta được:
\(BD^2=AB^2+AD^2\)
\(\Leftrightarrow AB^2=BD^2-AD^2=\left(4\sqrt{10}\right)^2-4^2=144\)
hay AB=12(cm)
Xét ΔABD vuông tại A có
\(\tan\widehat{ABD}=\dfrac{AD}{AB}=\dfrac{4}{12}=\dfrac{1}{3}\)
hay \(\widehat{ABD}\simeq18^026'\)
mà \(\widehat{ABC}=2\cdot\widehat{ABD}\)(BD là tia phân giác của \(\widehat{ABC}\))
nên \(\widehat{ABC}\simeq36^052'\)
Xét ΔABC vuông tại A có
\(AC=AB\cdot\tan\widehat{ABC}\)
\(\Leftrightarrow AC=12\cdot\tan36^052'\simeq9\)(cm)
Ta có: ΔABC vuông tại A(gt)
nên \(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{12\cdot9}{2}=\dfrac{108}{2}=54\left(cm^2\right)\)

xét tam giác ABD có góc BAD=90 độ
= BD^2=AB^2+AD^2
=>AB^2=BD^2-AD^2=10-1=9
=> AB=3 cm
có AC=AD+DC=1+√10 cm
tam giác ABC vuông tại A
=>AB^2+AC^2=BC^2
=>BC^2=9+1+2√10+10=20+2√10
=>BC=√(20+2√10)
Cho tam giác ABC(góc A= 90 độ)
BD là phân giác của góc B
AD= 1cm
BD=\(\sqrt{10}cm\)
Tính BC
giúp mình với


Lời giải:
Theo tính chất tia phân giác:
$\frac{AB}{BC}=\frac{AD}{DC}=\frac{4\sqrt{10}}{5\sqrt{10}}=\frac{4}{5}$
$AC=4\sqrt{10}+5\sqrt{10}=9\sqrt{10}$
Áp dụng định lý Viet:
$BC^2=AB^2+AC^2$
$\Leftrightarrow (\frac{5}{4}AB)^2=AB^2+(9\sqrt{10})^2$
$\Leftrightarrow AB^2=1440$
$BD=\sqrt{AB^2+AD^2}=\sqrt{1440+(4\sqrt{10})^2}=\sqrt{1440+160}=40$ (cm)
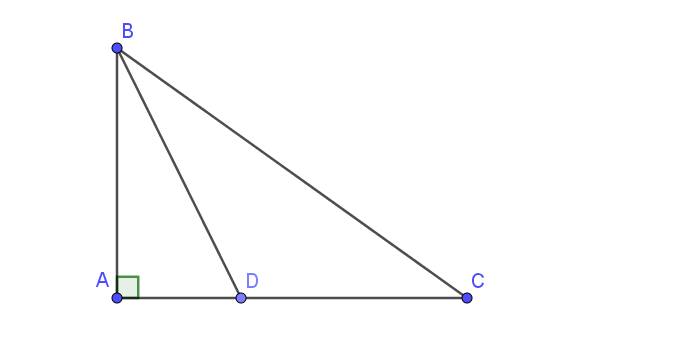
Áp dụng định lí Pytago vào ΔABD vuông tại A, ta được:
\(BD^2=AD^2+AB^2\)
\(\Leftrightarrow AB^2=BD^2-AD^2=\left(\sqrt{10}\right)^2-1^2=9\)
hay AB=3(cm)
Xét ΔABD vuông tại A có
\(\sin\widehat{ABD}=\dfrac{AD}{BD}=\dfrac{1}{\sqrt{10}}\)
nên \(\widehat{ABD}\simeq18^026'\)
mà \(\widehat{ABC}=2\cdot\widehat{ABD}\)(BD là tia phân giác của \(\widehat{ABC}\))
nên \(\widehat{ABC}\simeq2\cdot18^026'=36^052'\)
Xét ΔABC vuông tại A có
\(AB=BC\cdot\cos\widehat{ABC}\)
\(\Leftrightarrow BC=\dfrac{AB}{\cos\widehat{ABC}}=\dfrac{3}{\cos36^052'}\)
hay \(BC\simeq3.75cm\)
Vậy: \(BC\simeq3.75cm\)