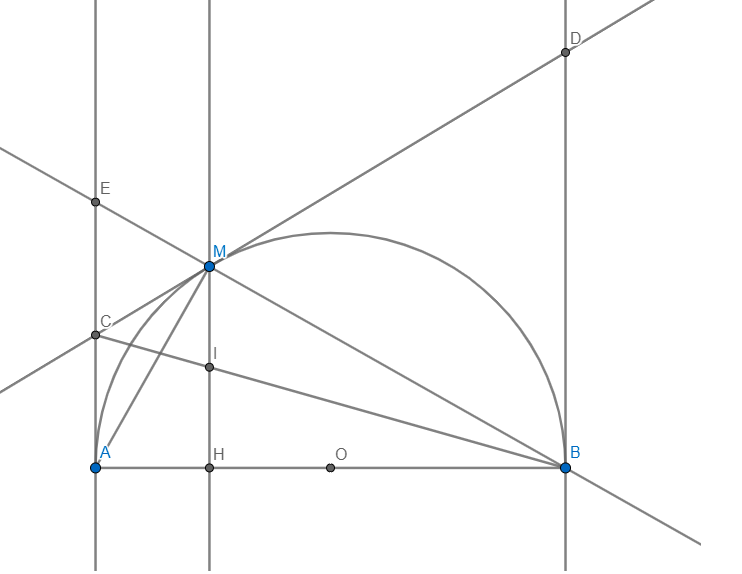
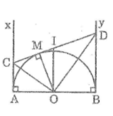
Cho đường tròn (O) đường kính AB, Ax và By là hai tiếp tuyến của (O) tại các tiếp điểm A, B. Lấy điểm M bất kì trên nửa đường tròn (M thuộc cùng một nửa mặt phẳng bờ AB chứa Ax, By), tiếp tuyến tại M của (O) cắt Ax, By lần lượt tại C và D.
1. Chứng minh: Tứ giác AOMC nội tiếp.
2. Giả sử BD = R√3. Tính AM.
3. Nối OC cắt AM tại E, OD cắt BM tại F, kẻ MN ⊥ AB (N ∈ AB), chứng minh đường tròn ngoại tiếp ΔNEF luôn đi qua 1 điểm cố định.
4. Tìm vị trí điểm M trên nửa đường tròn để bán kính đường tròn ngoại tiếp tứ giác CEFD có độ dài nhỏ nhất