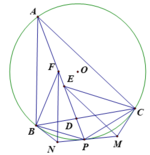
Cho \(\Delta ABC\) có 3 góc nhọn nội tiếp (O). Tiếp tuyến tại B và C của đường tròn cắt nhau tại D.Từ D kẻ đường thẳng song song với AB, đường thẳng này cắt (O) tại E,F và cắt AC tại I \(\left(E\in\stackrel\frown{BC\text{ nhỏ}}\right)\)
a, Chứng minh: Tứ giác BDCO nội tiếp
b,Chứng minh: DC2=DE.DF
c,Chứng minh DOIC nội tiếp
d, Chứng minh I là trung điểm FE