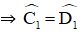Cho tứ giác ABCD có E là giao điểm hai đường chéo. Tính AD biết rằng AB=6, EA=8, EB=4 , ED=6
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tam giác ABI có cạnh AB < AI => góc ABI > góc AIB
Kẻ AH vuông góc với BD . Đặt BH = x; AH = y
+) Nếu H nằm trong đoạn BI
Áp dụng ĐL Pi ta go trong tam giác vuông AHB có: AH2 + BH2 = AB2 => y2 + x2 = 36 (1)
HI = 4 - x
Áp dụng ĐL Pi ta go trong tam giác vuông AHI có: AH2 + HI2 = AI2 => y2 + (4 - x)2 = 64 => y2 + x2 + 16 - 8x = 64 (2)
Từ (1)(2) => 36 + 16 - 8x = 64 => 8x = -12 => Loại
=> H nằm ngoài đoạn BI về phía B
HI = x + 4
Áp dụng ĐL Pi ta go trong tam giác vuông AHI có: AH2 + HI2 = AI2 => y2 + (x+ 4)2 = 64 => y2 + x2 + 8x + 16 = 64 (3)
Từ (1)(3) => 36 + 16 + 8x = 64 => 8x = 12 => x = 1,5
=> y2 = 33,75
HD = x + 4 + 6 = 11,5
Áp dụng ĐL Pita go trong tam giác vuông AHD có: AD2 = y2 + HD2 => AD2 = 33,75 + 11,52 = 166 => AD = \(\sqrt{166}\approx12,88\) (cm)

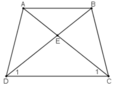
Do ABCD là hình thang cân nên:
AD = BC;
AC = BD;
Xét hai tam giác ADC và BCD, ta có:
AD = BC (gt)
AC = BD (gt)
DC cạnh chung
⇒ ΔADC = ΔBCD (c.c.c)
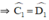
⇒ ΔECD cân tại E
⇒ EC = ED.
Mà AC = BD
⇒ AC – EC = BD – ED
hay EA = EB.
Vậy EA = EB, EC = ED.

Bài giải:
Do ABCD là hình thang cân nên AD = BC, AC = BC,
Xét hai tam giác ADC và BCD, ta có: 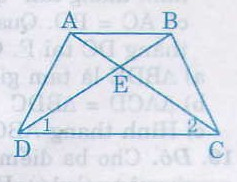
AD = BC (gt)
AC = BD (gt)
DC chung
Nên ∆ADC = ∆BCD (c.c.c)
Suy ra
Do đó tam giác ECD cân tại E, nên EC = ED
Ta lại có: AC = BD suy ra EA = EB
Chú ý: Ngoài cách chứng minh ∆ADC = ∆BCD (c.c.c) ta còn có thể chứng minh ∆ADC = ∆BCD (c.g.c) như sau:
AD = BC, , DC là cạnh chung.

Do ABCD là hình thang cân nên:
AD = BC;
AC = BD;
Xét hai tam giác ADC và BCD, ta có:
AD = BC (gt)
AC = BD (gt)
DC cạnh chung
⇒ ΔADC = ΔBCD (c.c.c)
⇒ ΔECD cân tại E
⇒ EC = ED.
Mà AC = BD
⇒ AC – EC = BD – ED
hay EA = EB.
Vậy EA = EB, EC = ED.

Do ABCD là hình thang cân nên AD = BC, AC = BC,
Xét hai tam giác ADC và BCD, ta có:
AD = BC (gt)
AC = BD (gt)
DC chung
Nên ∆ADC = ∆BCD (c.c.c)
Suy ra
Do đó tam giác ECD cân tại E, nên EC = ED
Ta lại có: AC = BD suy ra EA = EB
Chú ý: Ngoài cách chứng minh ∆ADC = ∆BCD (c.c.c) ta còn có thể chứng minh ∆ADC = ∆BCD (c.g.c) như sau:
AD = BC, , DC là cạnh chung.
Do ABCD là hình thang cân nên:
AD = BC;
AC = BD;
Xét hai tam giác ADC và BCD, ta có:
AD = BC (gt)
AC = BD (gt)
DC cạnh chung
⇒ ΔADC = ΔBCD (c.c.c)
⇒ ΔECD cân tại E
⇒ EC = ED.
Mà AC = BD
⇒ AC – EC = BD – ED
hay EA = EB.
Vậy EA = EB, EC = ED.

Do ABCD là hình thang cân nên:
AD = BC;
AC = BD;
Xét hai tam giác ADC và BCD, ta có:
AD = BC (gt)
AC = BD (gt)
DC cạnh chung
⇒ ΔADC = ΔBCD (c.c.c)
⇒ ΔECD cân tại E
⇒ EC = ED.
Mà AC = BD
⇒ AC – EC = BD – ED
hay EA = EB.
Vậy EA = EB, EC = ED.