Cho \(\Delta ABC=\Delta MNP\) biết góc B=60 độ, góc P=30 độ
a) CMR: \(\Delta ABC,\Delta MNP\) là các tam giác vuông
b) Vẽ MK vuông NP. Tính số đo góc NMK và góc PMK
Mk đag cần gấp, có ai giải giúp mk hk
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 2 2019
Bài làm
a) Vì tam giác ABC = tam giác MNP ( giả thiết )
=> \(\widehat{N}=\widehat{B}=60^0\)
\(\widehat{M}=\widehat{A}\)
\(\widehat{P}=\widehat{C}=30^o\)
Xét tam giác ABC có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)( Định lý tổng ba góc của tam giác )
=> \(\widehat{A}=180^o-\widehat{B}-\widehat{C}\)
hay \(\widehat{A}=180^o-60^o-30^o\)
=> \(\widehat{A}=90^o\)
=> Tam giác ABC vuông tại A
Mà \(\widehat{A}=\widehat{M}\)( Chứng minh trên )
=> Tam giác MNP vuông tại M
b) Vì MK vuông góc với NP
=> tam giác MKN là tam giác vuông
=> \(\widehat{MAN}=90^o\)
Xét tam giác MKN vuông tại K
có: \(\widehat{N}+\widehat{NMK}=90^o\)( Hai góc phụ nhau )
hay \(60^o+\widehat{NMK}=90^o\)
=> \(\widehat{NMK}=90^o-60^o\)
=> \(\widehat{NMK}=30^o\)
Vậy \(\widehat{NMK}=30^o\)
Vì \(\widehat{NMP}=90^o\)( Chứng minh trên )
Ta có: \(\widehat{NMK}+\widehat{PKM}=\widehat{NMP}\)
hay \(30^o+\widehat{PKM}=90^o\)
=> \(\widehat{PKM}=90^o-60^o\)
=> \(\widehat{PKM}=30^o\)
Vậy \(\widehat{PKM}=30^o\)
~ Bạn ghi nhầm đề bài ak, nếu là tính góc PNK thì sai nha ~
# Chúc bạn học tốt #
H9
HT.Phong (9A5)
CTVHS
5 tháng 10 2023
Do: \(\Delta ABC=\Delta MNP\left(gt\right)\)
\(\Rightarrow\widehat{A}=\widehat{M}=40^o\) (hai góc tương ứng)
Mà: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow\widehat{B}+\widehat{C}=180^o-40^o=140^o\)
\(\Rightarrow3\widehat{B}+3\widehat{C}=3\cdot140^o\)
Lại có: \(3\widehat{B}=4\widehat{C}\)
\(\Rightarrow4\widehat{C}+3\widehat{C}=420^o\)
\(\Rightarrow7\widehat{C}=420^o\Rightarrow\widehat{C}=60^o\)
\(\Rightarrow\widehat{\text{B}}=140^o-60^o=80^o\)
KV
5 tháng 10 2023
Do ∆ABC = ∆MNP (gt)
⇒ ∠A = ∠M = 40⁰
Ta có:
∠A + ∠B + ∠C = 180⁰ (tổng ba góc trong ∆ABC)
⇒ ∠B + ∠C = 180⁰ - ∠A
= 180⁰ - 40⁰
= 140⁰
⇒ 3(∠B + ∠C) = 3.140⁰
⇒ 3∠B + 3∠C = 420⁰
Mà 3∠B = 4∠C
⇒ 4∠C + 3∠C = 420⁰
⇒ 7∠C = 420⁰
⇒ ∠C = 420⁰ : 7
⇒ ∠C = 60⁰
⇒ ∠B = 140⁰ - ∠C
= 140⁰ - 60⁰
= 80⁰
Vậy số đo các góc của ∆ABC là:
∠A = 40⁰; ∠B = 80⁰; ∠C = 60⁰
17 tháng 9 2023
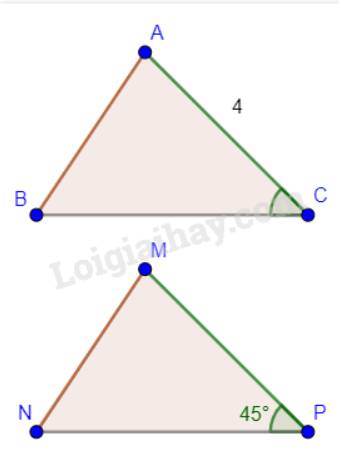
\(\Delta ABC = \Delta MNP\) nên \(AC = MP\)và \(\widehat {MPN} = \widehat {ACB}\).
Vậy \(MP = 4\)cm và \(\widehat {ACB} = 45^\circ \).
HP
2
MA
16 tháng 8 2015
vì tam giác ABC = tam giác MNP
=> góc B = góc N ( tương ứng )
=> góc N = 50 độ
ta có góc M +góc N + góc P = 180độ( tổng 3 góc của 1 tam giác)
góc P = 180 - M -N
P =180 -30 -50
P =100 độ
17 tháng 9 2023
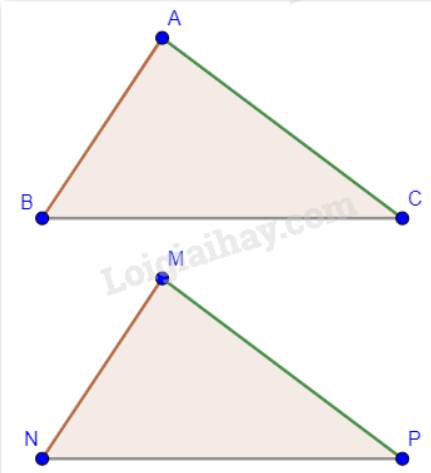
Ta có: \(\Delta ABC = \Delta MNP\) nên \(\widehat A = \widehat M,\widehat B = \widehat N,\widehat C = \widehat P\).
Mà \(\widehat A + \widehat N = 125^\circ \)hay \(\widehat M + \widehat N = 125^\circ \). Tổng ba góc trong một tam giác bằng 180°.
Trong tam giác MNP:
\(\begin{array}{l}\widehat M + \widehat N + \widehat P = 180^\circ \\125^\circ + \widehat P = 180^\circ \\ \to \widehat P = 180^\circ - 125^\circ = 55^\circ \end{array}\)
Vậy số đo góc P là 55°.
14 tháng 1 2022
a: \(\widehat{P}=180^0-45^0-35^0=100^0\)
b: Số đo góc ngoài tại đỉnh N là:
\(\widehat{P}+\widehat{M}=100^0+45^0=145^0\)
13 tháng 12 2016
Ta có hình vẽ:
a/ Trong tam giác ABC có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
hay 900 + góc B + 400 = 1800
=> góc ABC = 500
Ta có: \(\widehat{ABD}\)=\(\widehat{DBC}\)=\(\frac{1}{2}\widehat{ABC}\)= \(\frac{1}{2}\)500 = 250
Vậy góc ABD = 250
b/ Xét tam giác ABD và tam giác EBD có:
\(\widehat{ABD}=\widehat{DBE}\) (GT)
BD: chung
AB = EB (GT)
Vậy tam giác ABD = tam giác EBD (c.g.c)
Ta có: tam giác ABD = tam giác EBD
=> \(\widehat{A}=\widehat{E}=90^0\) hay DE \(\perp\)BC (đpcm)
c/ Xét tam giác ABC và tam giác EBF có:
\(\widehat{B}\): góc chung
BA = BE (GT)
góc A = góc E = 900 (đã chứng minh trên)
=> tam giác ABC = tam giác EBF
(trường hợp cạnh huyền góc nhọn)
d/ Xét tam giác BFK và tam giác BCK có:
BK: cạnh chung
\(\widehat{FBK}=\widehat{CBK}\) (GT)
BF = BC (tam giác ABC = tam giác EBF)
=> tam giác BFK = tam giác BCK (c.g.c)
=> \(\widehat{BKF}\)=\(\widehat{BKC}\) (2 góc tương ứng)
Mà góc BKC = 900 (do CK\(\perp\)BD) => góc BKF = 900
Ta có: \(\widehat{FKC}=\widehat{BKF}+\widehat{BKC}=90^0+90^0=180^0\)
hay K,F,C thẳng hàng
15 tháng 12 2016
d) ta có tam giác ABC = tam giác EBF ( theo c)
=> BC = BF ( 2 cạnh tương ứng)
Xét tam giác BKC và tam giác BKF có:
BC = BF ( gt )
BK chung
KBK = FBC ( gt)
=> tam giác BKC = tam giác BKF ( c.g.c )
=> BKC = BKF ( 2 góc tương ứng)
=> BKC + BKF = 180°( 2 góc kề bù)
=> BKC = BKF = 180° : 2 = 90° = FKC
vậy 3 điểm F,K,C thẳng hàng
Vì \(\Delta ABC=\Delta MNP\) nên:
N = B = 60o (2 góc tương ứng)
C = P = 30o (2 góc tương ứng)
Nên A = M = 180o - (60o + 30o) = 90o
Vậy \(\Delta ABC,\Delta MNP\) là các tam giác vuông (có góc bằng 90o)