Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài làm
a) Vì tam giác ABC = tam giác MNP ( giả thiết )
=> \(\widehat{N}=\widehat{B}=60^0\)
\(\widehat{M}=\widehat{A}\)
\(\widehat{P}=\widehat{C}=30^o\)
Xét tam giác ABC có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)( Định lý tổng ba góc của tam giác )
=> \(\widehat{A}=180^o-\widehat{B}-\widehat{C}\)
hay \(\widehat{A}=180^o-60^o-30^o\)
=> \(\widehat{A}=90^o\)
=> Tam giác ABC vuông tại A
Mà \(\widehat{A}=\widehat{M}\)( Chứng minh trên )
=> Tam giác MNP vuông tại M
b) Vì MK vuông góc với NP
=> tam giác MKN là tam giác vuông
=> \(\widehat{MAN}=90^o\)
Xét tam giác MKN vuông tại K
có: \(\widehat{N}+\widehat{NMK}=90^o\)( Hai góc phụ nhau )
hay \(60^o+\widehat{NMK}=90^o\)
=> \(\widehat{NMK}=90^o-60^o\)
=> \(\widehat{NMK}=30^o\)
Vậy \(\widehat{NMK}=30^o\)
Vì \(\widehat{NMP}=90^o\)( Chứng minh trên )
Ta có: \(\widehat{NMK}+\widehat{PKM}=\widehat{NMP}\)
hay \(30^o+\widehat{PKM}=90^o\)
=> \(\widehat{PKM}=90^o-60^o\)
=> \(\widehat{PKM}=30^o\)
Vậy \(\widehat{PKM}=30^o\)
~ Bạn ghi nhầm đề bài ak, nếu là tính góc PNK thì sai nha ~
# Chúc bạn học tốt #

Do: \(\Delta ABC=\Delta MNP\left(gt\right)\)
\(\Rightarrow\widehat{A}=\widehat{M}=40^o\) (hai góc tương ứng)
Mà: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow\widehat{B}+\widehat{C}=180^o-40^o=140^o\)
\(\Rightarrow3\widehat{B}+3\widehat{C}=3\cdot140^o\)
Lại có: \(3\widehat{B}=4\widehat{C}\)
\(\Rightarrow4\widehat{C}+3\widehat{C}=420^o\)
\(\Rightarrow7\widehat{C}=420^o\Rightarrow\widehat{C}=60^o\)
\(\Rightarrow\widehat{\text{B}}=140^o-60^o=80^o\)
Do ∆ABC = ∆MNP (gt)
⇒ ∠A = ∠M = 40⁰
Ta có:
∠A + ∠B + ∠C = 180⁰ (tổng ba góc trong ∆ABC)
⇒ ∠B + ∠C = 180⁰ - ∠A
= 180⁰ - 40⁰
= 140⁰
⇒ 3(∠B + ∠C) = 3.140⁰
⇒ 3∠B + 3∠C = 420⁰
Mà 3∠B = 4∠C
⇒ 4∠C + 3∠C = 420⁰
⇒ 7∠C = 420⁰
⇒ ∠C = 420⁰ : 7
⇒ ∠C = 60⁰
⇒ ∠B = 140⁰ - ∠C
= 140⁰ - 60⁰
= 80⁰
Vậy số đo các góc của ∆ABC là:
∠A = 40⁰; ∠B = 80⁰; ∠C = 60⁰

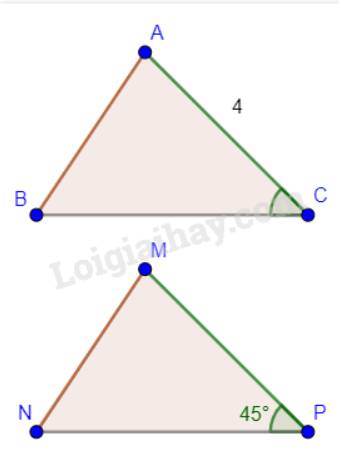
\(\Delta ABC = \Delta MNP\) nên \(AC = MP\)và \(\widehat {MPN} = \widehat {ACB}\).
Vậy \(MP = 4\)cm và \(\widehat {ACB} = 45^\circ \).

vì tam giác ABC = tam giác MNP
=> góc B = góc N ( tương ứng )
=> góc N = 50 độ
ta có góc M +góc N + góc P = 180độ( tổng 3 góc của 1 tam giác)
góc P = 180 - M -N
P =180 -30 -50
P =100 độ

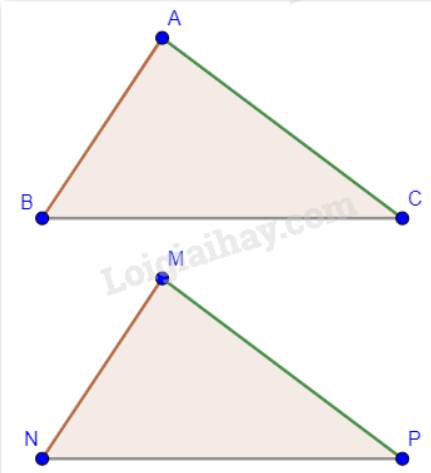
Ta có: \(\Delta ABC = \Delta MNP\) nên \(\widehat A = \widehat M,\widehat B = \widehat N,\widehat C = \widehat P\).
Mà \(\widehat A + \widehat N = 125^\circ \)hay \(\widehat M + \widehat N = 125^\circ \). Tổng ba góc trong một tam giác bằng 180°.
Trong tam giác MNP:
\(\begin{array}{l}\widehat M + \widehat N + \widehat P = 180^\circ \\125^\circ + \widehat P = 180^\circ \\ \to \widehat P = 180^\circ - 125^\circ = 55^\circ \end{array}\)
Vậy số đo góc P là 55°.

a: \(\widehat{P}=180^0-45^0-35^0=100^0\)
b: Số đo góc ngoài tại đỉnh N là:
\(\widehat{P}+\widehat{M}=100^0+45^0=145^0\)

Ta có hình vẽ:
a/ Trong tam giác ABC có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
hay 900 + góc B + 400 = 1800
=> góc ABC = 500
Ta có: \(\widehat{ABD}\)=\(\widehat{DBC}\)=\(\frac{1}{2}\widehat{ABC}\)= \(\frac{1}{2}\)500 = 250
Vậy góc ABD = 250
b/ Xét tam giác ABD và tam giác EBD có:
\(\widehat{ABD}=\widehat{DBE}\) (GT)
BD: chung
AB = EB (GT)
Vậy tam giác ABD = tam giác EBD (c.g.c)
Ta có: tam giác ABD = tam giác EBD
=> \(\widehat{A}=\widehat{E}=90^0\) hay DE \(\perp\)BC (đpcm)
c/ Xét tam giác ABC và tam giác EBF có:
\(\widehat{B}\): góc chung
BA = BE (GT)
góc A = góc E = 900 (đã chứng minh trên)
=> tam giác ABC = tam giác EBF
(trường hợp cạnh huyền góc nhọn)
d/ Xét tam giác BFK và tam giác BCK có:
BK: cạnh chung
\(\widehat{FBK}=\widehat{CBK}\) (GT)
BF = BC (tam giác ABC = tam giác EBF)
=> tam giác BFK = tam giác BCK (c.g.c)
=> \(\widehat{BKF}\)=\(\widehat{BKC}\) (2 góc tương ứng)
Mà góc BKC = 900 (do CK\(\perp\)BD) => góc BKF = 900
Ta có: \(\widehat{FKC}=\widehat{BKF}+\widehat{BKC}=90^0+90^0=180^0\)
hay K,F,C thẳng hàng
d) ta có tam giác ABC = tam giác EBF ( theo c)
=> BC = BF ( 2 cạnh tương ứng)
Xét tam giác BKC và tam giác BKF có:
BC = BF ( gt )
BK chung
KBK = FBC ( gt)
=> tam giác BKC = tam giác BKF ( c.g.c )
=> BKC = BKF ( 2 góc tương ứng)
=> BKC + BKF = 180°( 2 góc kề bù)
=> BKC = BKF = 180° : 2 = 90° = FKC
vậy 3 điểm F,K,C thẳng hàng
Vì \(\Delta ABC=\Delta MNP\) nên:
N = B = 60o (2 góc tương ứng)
C = P = 30o (2 góc tương ứng)
Nên A = M = 180o - (60o + 30o) = 90o
Vậy \(\Delta ABC,\Delta MNP\) là các tam giác vuông (có góc bằng 90o)