Help Me!!!
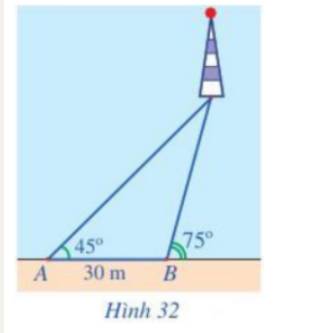
Từ vị trí A người ta quan sát 1 cái cây cao
Biết AH = 4m, HB = 20m, BAC = 45o.
Tính BC = ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 6 2018
Gọi chiều cai của xây là x(m) (x>0)
Áp dụng công thức
\(\frac{200}{50}\)=\(\frac{x}{400}\)
Từ đó tìm đk x=1600cm=16m(tmđk của x)
CHỌN A
N
30 tháng 4 2022
Ta có: \(OA'=d'=2cm\), người này quan sát thấy cái tháp cao 5m nên \(h=5m=500cm\) và khoảng cách từ tháp đến người này là 30 cm nên \(d=30cm\).
Chiều cao của ảnh trên màng lưới:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow h'=\dfrac{h\cdot d'}{d}=\dfrac{500\cdot2}{30}\approx33,\left(3\right)cm\)
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
Gọi C là vị trí ngọn hải đăng và H là hình chiếu của C trên AB.
Khi đó CH là khoảng cách từ ngọn hải đăng tới bờ biển.
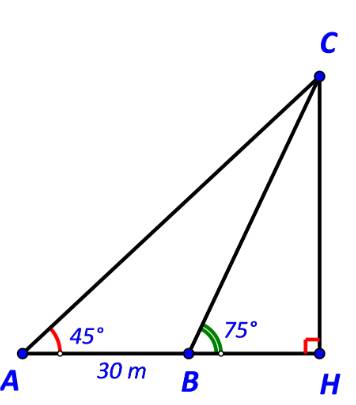
Ta có: \( \widehat {ACB} = \widehat {HBC} - \widehat {BAC} = {75^o} - {45^o} = {30^o}; \, \widehat {ABC} = {180^o} - {75^o} = {105^o}\)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}\)
\( \Rightarrow AC = \sin B.\frac{{AB}}{{\sin C}} = \sin {105^o}.\frac{{30}}{{\sin {{30}^o}}} \approx 58\)
Tam giác ACH vuông tại H nên ta có:
\(CH = \sin A.AC = \sin {45^o}.58 \approx 41\)
Vậy ngọn hải đăng cách bờ biển 41 m.
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 3 2023
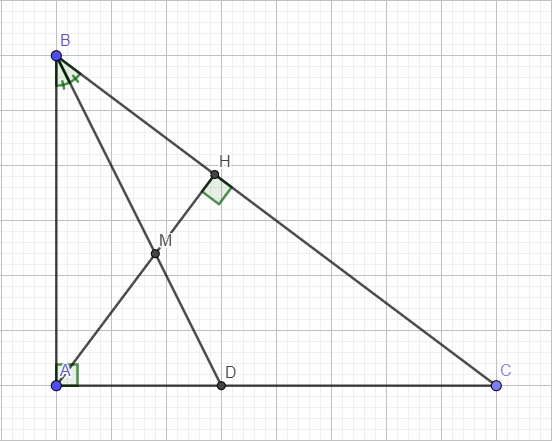
a.
Xét hai tam giác BAC và BHA có:
\(\left\{{}\begin{matrix}\widehat{ABH}\text{ chung}\\\widehat{BAC}=\widehat{BHA}=90^0\end{matrix}\right.\)
\(\Rightarrow\Delta BAC\sim\Delta BHA\left(g.g\right)\)
b.
Áp dụng định lý Pitago cho tam giác vuông ABC:
\(BC^2=AB^2+AC^2\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+4^2}=5\)
Do \(\Delta BAC\sim\Delta BHA\Rightarrow\dfrac{BC}{AB}=\dfrac{AC}{AH}\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{3.4}{5}=\dfrac{12}{5}\)
Áp dụng định lý Pitago cho tam giác vuông ABH:
\(BH=\sqrt{AB^2-AH^2}=\dfrac{9}{5}\)
\(CH=BC-BH=\dfrac{16}{5}\)
c.
Do BD là phân giác góc B, áp dụng định lý phân giác cho tam giác ABC:
\(\dfrac{DC}{AD}=\dfrac{BC}{AB}\) (1)
Áp dụng định lý phân giác cho tam giác ABH:
\(\dfrac{AM}{HM}=\dfrac{AB}{BH}\) (2)
Lại có \(\Delta BAC\sim\Delta BHA\Rightarrow\dfrac{BC}{AB}=\dfrac{AB}{BH}\) (3)
(1);(2);(3) \(\Rightarrow\dfrac{DC}{AD}=\dfrac{AM}{HM}\Rightarrow AM.AD=HM.CD\)
Tam giác \(AHB\) vuông tại $H$ nên $AB^2=AH^2+HB^2=4^2+20^2=416$
\(\Rightarrow AB \approx 20,4\)
\(tan\widehat {BAH} = \frac{{HB}}{{HA}} = \frac{{20}}{4} = 5\\ \Rightarrow {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \widehat {BAH} \approx {78,7^0}\\ \Rightarrow {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \widehat {HAC} \approx {78,7^0} + {45^0} \approx {123,7^0} \)
\( {\widehat {HAB} + \widehat {HBA} = {{90}^0}}\\ {\widehat {ABC} + \widehat {HBA} = {{90}^0}}\\ { \Rightarrow \widehat {HAB} = \widehat {ABC}}\\ { \Rightarrow \widehat {BCA} = {{180}^0}-\widehat {BAC}-\widehat {ABC} = {{180}^0}-\widehat {HAC}} \)
\( \Rightarrow {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \widehat {BCA} \approx {180^0}-{123,7^0} = {56,3^0}.\)
Ta có: \(\frac{{BC}}{{{\rm{sin}}{{45}^0}}} = \frac{{AB}}{{{\rm{sin}}{{56,3}^0}}}\)
\(\Rightarrow {\mkern 1mu} {\mkern 1mu} BC = \frac{{20,4}}{{{\rm{sin}}{{56,3}^0}}}{\rm{sin}}{45^0} \approx 17,4\)
Vậy \(BC\approx17,4m\)
Tam giác \(AHB\) vuông tại H nên \(A{B^2} = A{H^2} + H{B^2} = {4^2} + {20^2} = 416\)
\(\Rightarrow AB \approx 20,4\)
\(tan\widehat {BAH} = \frac{{HB}}{{HA}} = \frac{{20}}{4} = 5\\ \Rightarrow {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \widehat {BAH} \approx {78,7^0}\\ \Rightarrow {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \widehat {HAC} \approx {78,7^0} + {45^0} \approx {123,7^0} \)
\( {\widehat {HAB} + \widehat {HBA} = {{90}^0}}\\ {\widehat {ABC} + \widehat {HBA} = {{90}^0}}\\ { \Rightarrow \widehat {HAB} = \widehat {ABC}}\\ { \Rightarrow \widehat {BCA} = {{180}^0}-\widehat {BAC}-\widehat {ABC} = {{180}^0}-\widehat {HAC}} \)
\( \Rightarrow {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \widehat {BCA} \approx {180^0}-{123,7^0} = {56,3^0}.\)
Ta có: \(\frac{{BC}}{{{\rm{sin}}{{45}^0}}} = \frac{{AB}}{{{\rm{sin}}{{56,3}^0}}}\)
\(\Rightarrow {\mkern 1mu} {\mkern 1mu} BC = \frac{{20,4}}{{{\rm{sin}}{{56,3}^0}}}{\rm{sin}}{45^0} \approx 17,4\)
Vậy \(BC\approx17,4m\)