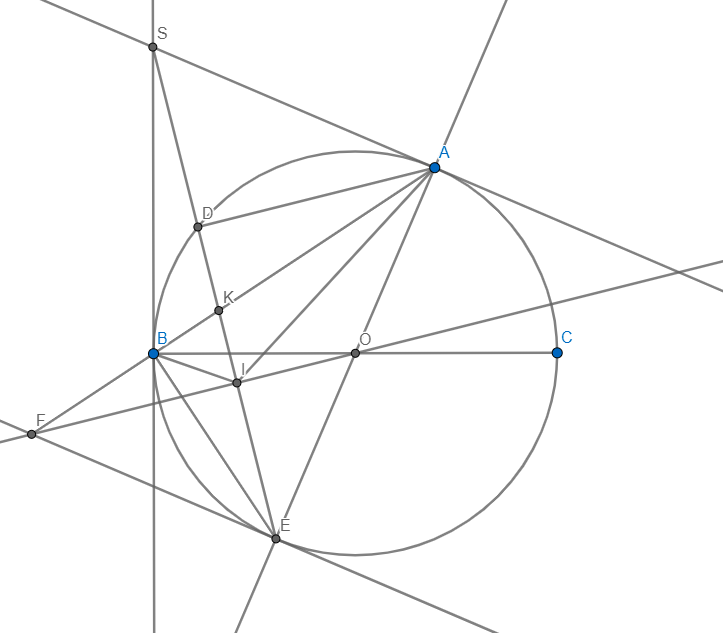
Cho ΔABCnhọn ( AB < BC ) nội tiếp dường tròn ( O

NQ

Nguyễn Quốc Huy

17 tháng 1 2019 - olm

Cho ΔABCnhọn ( AB < BC ) nội tiếp dường tròn ( O ;R ). Gọi M là điểm di động trên cung nhỏ BC. Vẽ AD vuông góc MB, AE vuông góc MC.Gọi H là giao điểm của DE và BC. â, CMR: A, H, E cùng thuộc 1 đường tròn và DE luôn đi qua 1 điểm cố địnhb, Xác định vị trí M để \(\frac{MB}{AD}.\frac{MC}{AE}\) đạt giá trị nhỏ nhất (hay lớn nhất j đó k nhớ nữa...

Đọc tiếp

#Toán lớp 9

0

N

nhocanime

27 tháng 4 2018 - olm

Cho tam giác nhọn ABC (AB<AC) nội tiếp đường tròn (O) dường kính AD. tiếp tuyến tại D của dường tròn cắt BC tại S. tia SO cắt AB,AC lần tược tại M,N. Gọi H là trung diểm của BC. Chứng minh OM=ON

#Toán lớp 9

0

PT

phạm tường vy channel

10 tháng 2 2020 - olm

CHO TAM GIÁC ABC CÓ BA GÓC NHỌN (AB<AC) NỘI TIẾP DƯỜNG TRÒN TÂM O. VẼ HAI ĐƯỜNG CAO BN VÀ CM CẮT NHAU TẠI HA/ CHỨNG MINH TỨ GIÁC AMHN VÀ TỨ GIÁC BMNC NỘI TIẾP DƯỜNG TRÒNB/ TIẾP TUYẾN TẠI A CẮT BC TẠI I. CHỨNG MINH IA MŨ 2 =IB*ICC/ DƯỜNG THẲNG MN CẮT DƯỜNG TRÒN TÂM O TẠI D VÀ E ( ĐIỂM M NẰM GIỮA HAI ĐIỂM D VÀ N ) CHỨNG MINH AD LÀ TIẾP TUYẾN CỦA ĐƯỜNG TRÒN NGOẠI TIẾPTAM GIÁC...

Đọc tiếp

#Toán lớp 9

0

PT

phạm tường vy channel

10 tháng 2 2020 - olm

CHO TAM GIÁC ABC CÓ BA GÓC NHỌN (AB<AC) NỘI TIẾP DƯỜNG TRÒN TÂM O. VẼ HAI ĐƯỜNG CAO BN VÀ CM CẮT NHAU TẠI HA/ CHỨNG MINH TỨ GIÁC AMHN VÀ TỨ GIÁC BMNC NỘI TIẾP DƯỜNG TRÒNB/ TIẾP TUYẾN TẠI A CẮT BC TẠI I. CHỨNG MINH IA MŨ 2 =IB*ICC/ DƯỜNG THẲNG MN CẮT DƯỜNG TRÒN TÂM O TẠI D VÀ E ( ĐIỂM M NẰM GIỮA HAI ĐIỂM D VÀ N ) CHỨNG MINH AD LÀ TIẾP TUYẾN CỦA ĐƯỜNG TRÒN NGOẠI TIẾPTAM GIÁC...

Đọc tiếp

#Toán lớp 9

0

TH

Thu Hiền Trần

4 tháng 5 2016 - olm

cho tam giác ABC (AB<AC) nội tiếp đường tròn (O) dường kính AD .tiếp tuyến tại D của đường tròn (O) cắt tia BC tại S .tia SO cắt AB,AC lần lượt tại M.N.gọi H là trung điểm của BC. chứng minh OM=ON

#Toán lớp 9

2

TH

Thu Hiền Trần

4 tháng 5 2016

làm ơn giúp với ạ

Đúng(0)

DQ

Đặng Quỳnh Ngân

4 tháng 5 2016

ta co tg AMDN la hinh binh hanh vi có góc đối = nhau tung doi mot

dg cheo AD ; NM cat nhau tai 0 nen OM =ON

Đúng(0)

W2

Wolf 2k6 has been cursed

26 tháng 6 2021

cho đường tròn O cò đường kính BC . trên đườn tròn O lấy điểm A sao cho AB>AC . vẽ các tiếp tuyến tại A,B của dường tròn O cắt nhau tại SA/ chứng minh tứ giác SAOB nội tiếp và SO vuông góc ABB/ kẻ đường kính AE của đườn tròn O , SE cắt đường tròn O tại D . chứng minh SD^2 = SD.SEC/ gọi I là rung điểm của DE , K là giao điểm của AB và SE . chứng minh SD.SE=SK.SID/ vẽ tiếp tuyến E của đường tròn O cắt tia...

Đọc tiếp

#Toán lớp 9

2

NL

Nguyễn Lê Phước Thịnh

26 tháng 6 2021

a) Xét tứ giác SAOB có

\(\widehat{SAO}+\widehat{SBO}=180^0\left(90^0+90^0=180^0\right)\)

nên SAOB là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

Xét (O) có

SA là tiếp tuyến có A là tiếp điểm(gt)

SB là tiếp tuyến có B là tiếp điểm(gt)

Do đó: SA=SB(Tính chất hai tiếp tuyến cắt nhau)

Ta có: SA=SB(cmt)

nên S nằm trên đường trung trực của AB(Tính chất đường trung trực của một đoạn thẳng)(1)

Ta có: OA=OB(=R)

nên O nằm trên đường trung trực của AB(Tính chất đường trung trực của một đoạn thẳng)(2)

Từ (1) và (2) suy ra SO là đường trung trực của AB

hay SO\(\perp\)AB(Đpcm)

Đúng(2)

AT

An Thy

28 tháng 6 2021

b) đề phải là \(SA^2=SD.SE\) chứ SD không bằng SE sao \(SD^2=SD.SE\) được

Vì AE là đường kính \(\Rightarrow\angle ADE=90\) mà \(\angle SAE=90\)

\(\Rightarrow\Delta SAE\) vuông tại A có AD là đường cao

\(\Rightarrow SA^2=SD.SE\)

c) Trong (O) có DE là dây cung không đi qua O và I là trung điểm DE

\(\Rightarrow OI\bot DE\Rightarrow\angle OIS=90\Rightarrow\angle OIS=\angle OBS=90\)

\(\Rightarrow OIBS\) nội tiếp mà SAOB nội tiếp (câu a)

\(\Rightarrow O,I,A,S,B\) cùng thuộc 1 đường tròn

\(\Rightarrow AIBS\) nội tiếp \(\Rightarrow\angle AIS=\angle ABS=\angle SAB\) (\(\Delta SAB\) cân tại S)

Xét \(\Delta SAK\) và \(\Delta SIA:\) Ta có: \(\left\{{}\begin{matrix}\angle SIA=\angle SAK\\\angle ISAchung\end{matrix}\right.\)

\(\Rightarrow\Delta SAK\sim\Delta SIA\left(g-g\right)\Rightarrow\dfrac{SA}{SI}=\dfrac{SK}{SA}\Rightarrow SA^2=SK.SI\)

mà \(SA^2=SD.SE\Rightarrow SD.SE=SK.SI\)

d) AB cắt OI tại F'

Vì AE là đường kính \(\Rightarrow\angle ABE=90\Rightarrow F'BE=90\)

\(\Rightarrow\angle F'BE=\angle F'IE\Rightarrow F'BIE\) nội tiếp \(\Rightarrow\angle ABI=\angle F'EI\)

mà \(\angle ABI=\angle ASI\) (AIBS nội tiếp) \(=\angle ASE\)

\(\Rightarrow\angle F'EI+\angle AES=\angle ASE+\angle AES=90\)

\(\Rightarrow\angle F'EO=90\Rightarrow EF'\) là tiếp tuyến \(\Rightarrow\) đpcm

undefined

Đúng(1)

NT

Nguyễn Thư

5 tháng 5 2021

cho tam giác ABC có 3 góc nhọn (AB<AC) nội tiếp đường tròn tâm O. Vẽ đường cao AD,BE,CF cắt nhau tại H

a) CM AFHE và BFEC là tứ giác nội tiếp

b) dường thẳng EF cắt BC tại I.CM IE.IF=IB.IC

c) AI cắt đường tròn tâm O tại K. M là trung điểm BC.CM 3 điểm K,H,M thẳng hàng

#Toán lớp 9

0

CD

chien dang

23 tháng 1 2020 - olm

cho tam giác nhọn (AB < AC) nội tiếp đường tròn (o) gọi H là trực tâm của tam giác ABC K laa2 giao điểm thứ hai của AH với dường tròn O đường thẳng đi qua H và vuông góc với OA cắt BC tại I chứng minh rằng IK là tiếp tuyến của dường tròn O

các bạn giải chi tiết hộ mình nha mình cảm ơn nhiều lắm

#Toán lớp 9

0

A

Acacia

23 tháng 1 2020 - olm

cho tam giác nhọn (AB < AC) nội tiếp đường tròn (o) gọi H là trực tâm của tam giác ABC K laa2 giao điểm thứ hai của AH với dường tròn O đường thẳng đi qua H và vuông góc với OA cắt BC tại I chứng minh rằng IK là tiếp tuyến của dường tròn O

các bạn giải chi tiết hộ mình nha mình cảm ơn nhiều lắm

#Toán lớp 9

0

TP

Tú phạm

28 tháng 5 2015 - olm

cho tam giác ABC có 3 góc nhọn nội tiếp trong đường tròn (O) (AB<AC). Dường tròn tâm O1 tiếp xúc trong với dường tròn (O) tại M, tiếp xúc với 2 cạnh AB, AC lần lượt tại L,K. Gọi E là giao điểm thứ hai của Mk với (O)
a/ c/m ME là tia phân giác góc AMC
b/tia phân giác Mx của góc BMC cắt LK tại I. CM rằng tứ giác MIKC nội tiếp

#Toán lớp 9

0

AT

Anh Thư ctue :))

14 tháng 4 2023

cho đường tròn (O,R) đường kính AB. Vẽ bán kính OC vuông góc với AB. Gọi M là một điểm trên OC; dường thẳng AM cắt dường tròn (o) tại N
a, Chứng minh tứ giác OMNB nội tiếp đường tròn
b, Xác định vị trí của M trên OC để tứ giác OMNB có hai đường chéo vuông góc với nhau.

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

14 tháng 4 2023

a:góc ANB=1/2*180=90 độ

góc MOB+góc MNB=180 độ

=>MNBO nội tiếp

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP