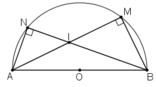
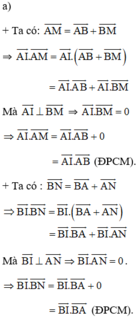Cho nửa đường tròn (O) đường kính AB = 2R. Gọi M, N là hai điểm di động trên nửa đường tròn sao cho M thuộc cung AN và tổng khoảng cách từ A và B đến đường thẳng MN bằng R√3. Ai giúp mình dựng hình với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi \(A',B'\)lần lượt là hình chiếu vuông góc của A, B lên MN, H là trung điểm của MN
\(\Rightarrow OH\perp MN\)
Xét hình thang \(AA'B'B\)có OH là đường trung bình nên:
\(OH=\frac{1}{2}\left(AA'+BB'\right)=\frac{R\sqrt{3}}{2}\)
\(MH=\sqrt{OM^2-OH^2}=\sqrt{R^2-\frac{3R^2}{4}}=\frac{R}{2}\)
\(\Rightarrow MN=2MH=R\)
do đó : \(S_{AKB}=\frac{1}{2}.AB.KP=R.KP\le\sqrt{3}R^2\)
Dấu "=" xảy ra <=> MN//AB hay \(\Delta AKB\)đều
b) bạn tự cm đc chứ ??? :))))
b,Tứ giác KMIN nội tiếp trong đường tròn đường kính KI, gọi Q là tâm đường tròn --> Q trung điểm KI ,
Vì MN = R , \(\Delta MNO\) đều
=> góc MAN = 30 độ
Trong tg vuông AKN có \(\widehat{MAN}\) = 300 => góc MKN = 60 độ -
=>góc MQN = 120 độ, vẽ QR vuông góc MN => R trung điểm MN => MR = R/2, trong tg MQR nửa đều
=> QR = MQ/2 và MR = R/2
=> MQ = \(R.\frac{\sqrt{3}}{3}\) --> Bán kính đường tròn = MQ =\(R.\frac{\sqrt{3}}{3}\)

Do I là trực tâm của tam giác KAB nên K, I, H thẳng hàng.
Tứ giác AMIH nội tiếp nên \(\widehat{MHI}=\widehat{MAI}\).
Tương tự, \(\widehat{NHI}=\widehat{NBI}\).
Lại có \(\widehat{MAI}=\widehat{NBI}=90^o-\widehat{AKB}\) nên \(\widehat{MHI}=\widehat{NHI}\).
Vậy HK là phân giác của góc MHN.

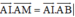 và
và 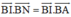
 theo R.
theo R.