Cho Δ ABC có A(-1;4), B(2,3), C(0,1)
a) lập pt tham số đường thẳng chứa cạnh AB
b) lập pt tổng quát đường cao BH
c) lập pt tổng quát trung tuyến CM
d) tìm tâm đường tròn ngoại tiếp Δ ABC
các bạn hãy giải giúp mình nhé!!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: C
Thay lần lượt tọa độ của ba điểm A, B, C vào đường thẳng Δ ta được:
A: 1 - 2.0 + 1 = 2 > 0
B: 2 - 2.(-3) + 1 = 9 > 0
C: -2 - 2.4 + 1 = -9 < 0
Ta thấy: A và C nằm khác phía so với Δ nên Δ cắt cạnh AC
B và C nằm khác phía so với Δ nên Δ cắt cạnh BC

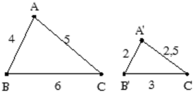
Xét Δ ABC,Δ A'B'C' có A'B'/AB = A'C'/AC = B'C'/BC = 2/4 = 2,5/5 = 3/6 = 1/2.
⇒ Δ ABC ∼ Δ A'B'C' ( c - c - c )

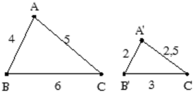
Xét Δ ABC,Δ A'B'C' có A'B'/AB = A'C'/AC = B'C'/BC = 2/4 = 2,5/5 = 3/6 = 1/2.
⇒ Δ ABC ∼ Δ A'B'C' ( c - c - c )

Áp dụng định lý Py – ta – go ta có: A C = ( B C 2 - A B 2 ) = ( 52 - 32 ) = 4 ( c m )
Δ ABC, AD là đường phân giác của góc BACˆ ( D ∈ BC )
Ta có: DB/DC = AB/AC hay DB/AB = DC/AC
Khi đó ta có: DB/DC = AB/AC ⇒ DB/( DB + DC ) = AB /( AB + AC )
hay DB/5 = 3/( 3 + 4) ⇒ DB = 15/7 cm; DC = 20/7 ( cm )
Chọn đáp án B.
a: \(\overrightarrow{AB}=\left(3;-1\right)\)
PT tham số là \(\left\{{}\begin{matrix}x=-1+3t\\y=4-t\end{matrix}\right.\)
b: Đường thẳng BH sẽ nhận vecto AC làm veto pháp tuyến
và đi qua B
\(\overrightarrow{AC}=\left(1;-3\right)\)
Phương trình BH là:
1(x-2)+(-3)*(y-3)=0
=>x-2-3y+9=0
=>x-3y+7=0