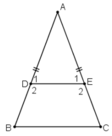
Cho △ABC cân tại A.Lấy D ∈ AB, E ∈ AC sao cho AD =AE.
a)Chứng minh rằng BDEC là hình thang cân
b)Lấy M là trung điểm của BD, N là trung điểm của EC.Biết MN = 3cm , BC = 4cm. Tính DE
c)Từ D kẻ DH // EC cắt MN tại K ( H ∈ BC) .Chứng minh : K là trung điểm của DH.Từ đó suy ra DH = EC = DB.


a: Xét ΔABC có AD/AB=AE/AC
nên DE//BC
=>BDEC là hìnhthang
mà góc B=góc C
nên BDEC là hình thang cân
b: Xét hình thang BDEC có
M,N lần lượt là trung điểm của DB và EC
nên MN là đường trung bình
=>MN=(DE+BC)/2
=>DE+4=6
=>DE=2cm
c: Xét tứ giác DECH có
DE//CH
DH//EC
Do đó: DECH là hình bình hành
SUy ra: DH=EC
Xét ΔDBH có MK//BH
nên DK/DH=DM/DB=1/2
=>K là trung điểm của DH