Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC có
D là trung điểm của AB
E là trung điểm của AC
Do đó: DE là đường trung bình
=>DE//BC và DE=BC/2
hay DE//BF và DE=BF
=>BDEF là hình bình hành
b: Xét tứ giác AMCF có
E là trung điểm của AC
E là trung điểm của MF
Do đó: AMCF là hình bình hành
mà \(\widehat{AMC}=90^0\)
nên AMCF là hình chữ nhật

a) Xét tứ giác AKCH có :
AD = DC ( D là trung điểm AC )
HD = DK ( K là điểm đối xứng của H qua D )
=> AKCH là hình bình hành (1)
Xét ∆ vuông AHC có :
HD là trung truyến
=> HD = AD = DC
Mà HD + DK = HK
AD + DC = AC
=> HK = AC (2)
Từ (1) và (2) => AKCH là hình chữ nhật
b) Xét ∆ABC có :
E là trung điểm AB
D là trung điểm BC
=> ED là đường trung bình ∆ABC
=> ED //BC
Xét ∆ABC có :
E là trung điểm AC
I là trung điểm BC
=> EI là đường trung bình ∆ABC
=> EI//AC , EI = \(\frac{1}{2}AC\)
Xét tứ giác EDCI có :
ED// IC ( I \(\in\)BC )
EI//DC ( D \(\in\)AC)
=> EDCI là hình bình hành
c) Vì ED //HI ( H , I \(\in\)BC )
=> EDIH là hình thang
Vì EI = \(\frac{1}{2}AC\)(cmt)
Mà HD = AD = DC (cmt)
=> HD = \(\frac{1}{2}AC\)
=> EI = HD
Mà EDIH là hình thang
=> EDIH là hình thang cân ( 2 đường chéo bằng nhau )

a, Vì I,M là trung điểm AC,BC nên IM là đtb tg ABC
Do đó IM//AB nên MIAB là hình thang
b, Xét tg ABC cân tại A có AM là trung tuyến nên cx là đg cao
Do đó AM⊥BC hay AM⊥CM(1)
Ta có I là trung điểm MK,AC nên AMCK là hbh
Kết hợp với (1) ta được AMCK là hcn
c, Vì AMCK là hcn nên \(MK=AC=AB\) (tg ABC cân tại A)
Mà MK//AB do MI//AB nên ABMK là hbh

a) Xét tứ giác EDCB có ED//BC(gt)
nên EDCB là hình thang có hai đáy là ED và BC(Định nghĩa hình thang)
Hình thang EDCB có \(\widehat{B}=\widehat{DCB}\)(hai góc ở đáy của ΔABC cân tại A)
nên EDCB là hình thang cân(Dấu hiệu nhận biết hình thang cân)
b) Xét tứ giác AKCH có
D là trung điểm của đường chéo AC(gt)
D là trung điểm của đường chéo HK(H và K đối xứng nhau qua D)
Do đó: AKCH là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Hình bình hành AKCH có \(\widehat{AHC}=90^0\)(AH⊥BC)
nên AKCH là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
c) Xét ΔABC cân tại A có AH là đường cao ứng với cạnh đáy BC(gt)
nên AH là đường trung tuyến ứng với cạnh BC(Định lí tam giác cân)
⇒H là trung điểm của BC
hay HB=HC
mà HC=AK(Hai cạnh đối trong hình chữ nhật AHCK)
nên BH=AK
Xét ΔABC có
H là trung điểm của BC(cmt)
D là trung điểm của AC(gt)
Do đó: HD là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
⇒HD//AB và \(HD=\dfrac{AB}{2}\)(Định lí 2 về đường trung bình của tam giác)(1)
Xét ΔABC có
D là trung điểm của AC(gt)
DE//BC(gt)
Do đó: E là trung điểm của AB(Định lí 1 về đường trung bình của tam giác)
⇒\(AE=\dfrac{AB}{2}\)(2)
Từ (1) và (2) suy ra HD//AE và HD=AE
Xét tứ giác AEHD có
HD//AE(cmt)
HD=AE(cmt)
Do đó: AEHD là hình bình hành(Dấu hiệu nhận biết hình bình hành)
⇒Hai đường chéo AH và ED cắt nhau tại trung điểm của mỗi đường(Định lí hình bình hành)
mà AH cắt ED tại F
nên F là trung điểm chung của AH và ED
Xét tứ giác AKHB có
AK//HB(AK//HC, B∈HC)
AK=HB(cmt)
Do đó: AKHB là hình bình hành(Dấu hiệu nhận biết hình bình hành)
⇒Hai đường chéo AH và BK cắt nhau tại trung điểm của mỗi đường(Định lí hình bình hành)
mà F là trung điểm của AH(cmt)
nên F là trung điểm của BK(đpcm)

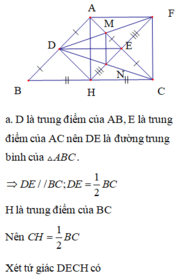


a: Xét ΔABC có
D là trung điểm của AB
E là trung điểm của AC
Do đó: DE là đường trung bình
=>DE//BC và DE=BC/2
Xét tứ giác BDEC có
DE//BC
nên BDEC là hình thang
mà \(\widehat{DBC}=\widehat{ECB}\)
nên BDEC là hình thang cân
b: Xét tứ giác AMCK có
E là trung điểm của AC
E là trung điểm của MK
Do đó: AMCK là hình bình hành
mà \(\widehat{AMC}=90^0\)
nên AMCK là hình chữ nhật