TÌM MIN VÀ MAX CỦA BIỂU THỨ SAU
\(P=\frac{-6X+1}{X^2+2X+3}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
S
13 tháng 7 2019
ĐKXĐ: \(x\ge1;y\ge25\)
\(D=\frac{1}{x}\sqrt{\frac{x-1}{\left(x-2\right)^2+25}}+\frac{1}{y}\sqrt{\frac{y-25}{\left(y-50\right)^2+1}}\)
Vì x>=1,y>=25 => x-1>=0,y-25>=0
=> D >= 0
Dấu "=" xảy ra <=> x=1,y=25
Vậy MinD=0 khi x=1,y=25
Ta có: \(\left(x-2\right)^2+25\ge25;\left(y-50\right)^2+1\ge1\)
=>\(\frac{1}{x}\sqrt{\frac{x-1}{\left(x-2\right)^2+25}}\le\frac{1}{x}\sqrt{\frac{x-1}{25}};\frac{1}{y}\sqrt{\frac{y-25}{\left(y-50\right)^2+1}}\le\frac{1}{y}\sqrt{y-25}\)
=>\(D\le\frac{1}{x}\sqrt{\frac{x-1}{25}}+\frac{1}{y}\sqrt{y-25}\)
Vì x>=1 => x-1>=0. Áp dụng bđt cosi với 2 số dương x-1 và 1 ta có:
\(\sqrt{x-1}=\sqrt{\left(x-1\right).1}\le\frac{x-1+1}{2}=\frac{x}{2}\)
=>\(\frac{1}{x}\sqrt{\frac{x-1}{25}}\le\frac{1}{x}\cdot\frac{x}{2}\cdot\frac{1}{\sqrt{25}}=\frac{1}{10}\)
Vì y>=25 => y-25>=0. ÁP dụng bđt cô si cho 2 số dương 25 và y-25 ta có:
\(\sqrt{y-25}=\frac{\sqrt{25\left(y-25\right)}}{5}\le\frac{25+y-25}{2.5}=\frac{y}{10}\)
=>\(\frac{1}{y}\sqrt{y-25}=\frac{1}{y}\cdot\frac{y}{10}=\frac{1}{10}\)
Suy ra \(D\le\frac{1}{10}+\frac{1}{10}=\frac{1}{5}\)
Dấu "=" xảy ra <=> x=2,y=50
Vậy MaxD = 1/5 khi x=2,y=50
23 tháng 12 2015
đúng đó trình bày lại đi xấu thật nhưng mik trình bày xấu hơn
8 tháng 9 2017
( a = 3; b =-4; c = 1)
TXĐ : D = R.
Tọa độ đỉnh I (2/3; -1/3).
Trục đối xứng : x = 2/3
Tính biến thiên :
a = 3 > 0 hàm số nghịch biến trên (-∞; 2/3). và đồng biến trên khoảng 2/3 ; +∞)
bảng biến thiên :
x | -∞ | 2/3 | +∞ | ||
y | +∞ | -1/3 | +∞ |
Các điểm đặc biệt :
(P) giao trục hoành y = 0 : 3x2 – 4x + 1 = 0 <=> x = 1 v x = ½
(P) giao trục tung : x = 0 => y = 1
Đồ thị :
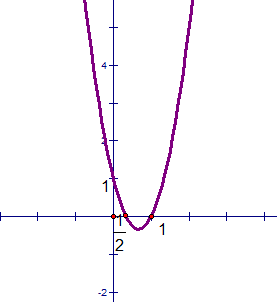
P/s: Bn tham khảo nhé, mk ko chắc đâu
H
21 tháng 3 2018
A lớn nhất khi \(3x^2+1\) nhỏ nhất.
Mà \(3x^2\ge0\)=> \(3x^2+1\ge1\)
Dấu = xảy ra khi : \(x=0\)
Khi đó \(A=\frac{6x-2}{3x^2+1}=\frac{-2}{1}=-2\)
21 tháng 3 2018
\(A=\frac{6x+1-3+3x^2-3x^2}{3x^2+1}=\frac{\left(3x^2+1\right)-3\left(1-2x+x^2\right)}{\left(3x^2+1\right)}=1-\frac{3\left(1-x\right)^2}{\left(3x^2+1\right)}\)
mà \(-3\left(1-x\right)^2\le0\)
\(\left(3x^2+1\right)>0\)
suy ra \(\frac{3\left(1-x\right)^2}{\left(3x^2+1\right)}\le0\Leftrightarrow1-\frac{3\left(1-x\right)^2}{\left(3x^2+1\right)}\le1\)
max của A là 1 dấu = xảy ra khi (1-x)=0 , x=1
HN
0
PT
0
20 tháng 9 2019
gợi ý thôi em câu này có gì khó đâu
c lớn hơn hoặc bằng 1
d nhỏ hơn hoặc = 10
trị tuyệt đối lớn lơn hoặc = 0
mẫu lớn số bé mẫu bé số lớn