Mọi người ơi giúp mình bài này với , thứ sáu mình đi học rồi :
Đề bài : Phân tích đa thức thành nhân tử theo cách đặt ẩn phụ : ( Cái nào tách được luôn thì các bạn ko cần đặt ẩn phụ đâu )
a) A = ( x2 + y2 + z2 )( x + y + z )2 + ( xy + yz + zx )2
b) B = x4 + x2 - 90
c) C = ( 5x2 - 2x )2 + 2x - 5x2 - 42
d) D = x2 + 8xy + 16y2 + 2x + 8y - 3
e) E = ( x2 + 3x + 1 )( x2 + 3x + 2 ) - 6
g) G = x16 + x8 - 2
h) H = ( x2 - 3x +1 )2- 12 ( x2 - 3 -1 ) +...
Đọc tiếp
Mọi người ơi giúp mình bài này với , thứ sáu mình đi học rồi :
Đề bài : Phân tích đa thức thành nhân tử theo cách đặt ẩn phụ : ( Cái nào tách được luôn thì các bạn ko cần đặt ẩn phụ đâu )
a) A = ( x2 + y2 + z2 )( x + y + z )2 + ( xy + yz + zx )2
b) B = x4 + x2 - 90
c) C = ( 5x2 - 2x )2 + 2x - 5x2 - 42
d) D = x2 + 8xy + 16y2 + 2x + 8y - 3
e) E = ( x2 + 3x + 1 )( x2 + 3x + 2 ) - 6
g) G = x16 + x8 - 2
h) H = ( x2 - 3x +1 )2- 12 ( x2 - 3 -1 ) + 27
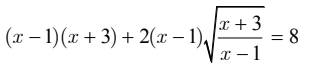( bài này giải theo phương pháp đặt ẩn phụ đúng không mọi người ? giải giúp mình với
b: \(=x^4+10x^2-9x^2-90\)
\(=\left(x^2+10\right)\left(x^2-9\right)\)
\(=\left(x^2+10\right)\left(x-3\right)\left(x+3\right)\)
c: \(=\left(5x^2-2x\right)^2-\left(5x^2-2x\right)-42\)
\(=\left(5x^2-2x-7\right)\left(5x^2-2x+6\right)\)
\(=\left(x-1\right)\left(5x+7\right)\left(5x^2-2x+6\right)\)
d: \(=\left(x+4y\right)^2+2\left(x+4y\right)-3\)
\(=\left(x+4y+3\right)\left(x+4y-1\right)\)
e: \(=\left(x^2+3x\right)^2+3\left(x^2+3x\right)-4\)
\(=\left(x^2+3x+4\right)\left(x^2+3x-1\right)\)