Cm:\(\dfrac{1+cos2a+sin2a}{1+sin2a-cos2a}=tana\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


(Sina -cosa)^2 =1:25
<=> sin^2a +cos^2a -2sina.cosa =1:25
Ta có sin^2a+cos^2a = 1
<=> 1-2 sina.cosa =1:25
2sina.cosa =24:25
CT : sin2a= 2sina.cosa=24:25
Có sin^2 .2a + co^2.2a = 1
(24:25)^2 + cos^2.2a =1
Từ đây rút cos 2a = căn 1-(24:25)^2 =... bạn tự làm tiếp nha !

\(\left(1+tan^2a\right)\left(1-sin^2a\right)-\left(1+cot^2a\right)\left(1-cos^2a\right)\)
\(=\left(1+\dfrac{sin^2a}{cos^2a}\right).cos^2a-\left(1+\dfrac{cos^2a}{sin^2a}\right).sin^2a\)
\(=cos^2a+sin^2a-sin^2a-cos^2a=\)\(0\)
Vậy B=0

Lời giải:
$\sin ^2a+\cos ^2a=1$
$\cos ^2a=1-\sin ^2a=1-(\frac{-5}{13})^2=\frac{144}{169}$
Vì $\pi < a< \frac{3\pi}{2}$ nên $\cos a< 0$
Do đó: $\cos a=-\sqrt{\frac{144}{169}}=\frac{-12}{13}$
$\sin 2a=2\sin a\cos a=2.\frac{-5}{13}.\frac{-12}{13}=\frac{120}{169}$
$\cos 2a=\cos ^2a-\sin ^2a=2\cos ^2a-1=2.\frac{144}{169}-1=\frac{119}{169}$
$\cos a=\cos ^2\frac{a}{2}-\sin ^2\frac{a}{2}$
$=1-2\sin ^2\frac{a}{2}$
$\Leftrightarrow \frac{-12}{13}=1-2\sin ^2\frac{a}{2}$
$\Rightarrow \sin ^2\frac{a}{2}=\frac{25}{26}$
Vì $\pi < a< \frac{3\pi}{2}$ nên $\sin \frac{a}{2}>0$
$\Rightarrow \sin \frac{a}{2}=\frac{5}{\sqrt{26}}$

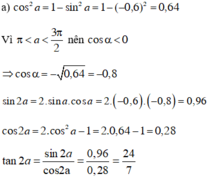
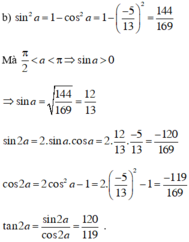
\(VT=\dfrac{1+\cos^2a-\sin^2a+2\cdot\sin a\cdot\cos a}{1+2\cdot\sin a\cdot\cos a-\cos^2a+\sin^2a}\)
\(=\dfrac{2\cdot\cos^2a+2\cdot\sin a\cdot\cos a}{2\cdot\sin^2a+2\cdot\sin a\cdot\cos a}\)
\(=\dfrac{2\cdot\cos a\left(\cos a+\sin a\right)}{2\cdot\sin a\cdot\left(\sin a+\cos a\right)}\)
\(=\dfrac{\cos a}{\sin a}=\cot a\)