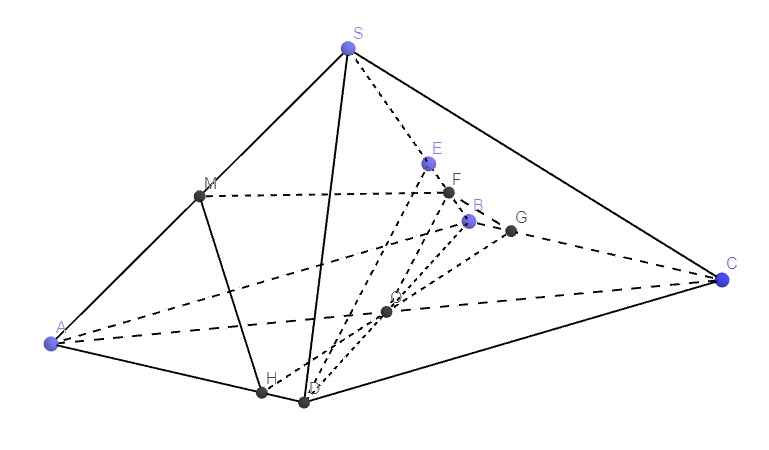
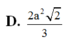Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Trong mặt phẳng (ABCD) vẽ
đường thẳng d đi qua A và không song song với các cạnh của hình bình hành. Trên cạnh SC lấy
điểm M. Tìm thiết diện của hình chóp khi cắt bởi mặt phẳng (M,d)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

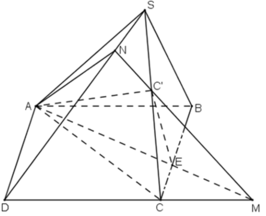
a) Giao điểm M của CD và mp(C’AE).
Trong mp(ABCD), d cắt CD tại M, ta có:
+ M ∈ CD
+ M ∈ d ⊂ (C’AE) ⇒ M ∈ (C’AE)
Vậy M là giao điểm của CD và mp(C’AE).
b) + Trong mặt phẳng (SCD), gọi giao điểm của MC’ và SD là N.
N ∈ MC’ ⊂ (C’AE) ⇒ N ∈ (C’AE).
N ∈ SD ⊂ (SCD) ⇒ N ∈ (SCD)
⇒ N ∈ (C’AE) ∩ (SCD).
⇒ (C’AE) ∩ (SCD) = C’N.
+ (C’AE) ∩ (SCB) = C’E.
+ (C’AE) ∩ (SAD) = AN.
+ (C’AE) ∩ (ABCD) = AE
Vậy thiết diện của hình chóp cắt bởi mặt phẳng (C’AE) là tứ giác C’NAE

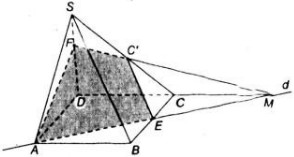
a) Trong (ABCD) gọi M = AE ∩ DC => M ∈ AE, AE ⊂ ( C'AE) => M ∈ ( C'AE). Mà M ∈ CD => M = DC ∩ (C'AE).
b)
Do M = DC ∩ (C'AE) nên M ∈ (SDC),.
Trong (SDC) : MC' ∩ SD = F.
Ta có:
\(\left(C'AE\right)\cap\left(SDC\right)=FC'\)
\(\left(C'AE\right)\cap\left(SAD\right)=AF\)
\(\left(C'AE\right)\cap\left(ABCD\right)=AE\)
\(\left(C'AE\right)\cap\left(SBC\right)=C'E\)
Vậy thiết diện là AEC'F.

Đáp án D
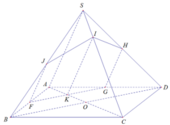
Trong (ABCD), kẻ đường thẳng d đi qua F và song song với BD
d cắt AD tại G
d cắt AC tại K ⇒ F G ∩ A C = K
Trong (SAD), kẻ đường thẳng x đi qua G và song song với SA
x cắt SD tại H
Trong (SAB), kẻ đường thẳng y đi qua F và song song với SA
y cắt SB tại J
Trong (SAC), kẻ đường thẳng z đi qua K và song song với SA
z cắt AC tại I
⇒ FGHIK là thiết diện cần tìm
⇒ thiết diện là ngũ giác

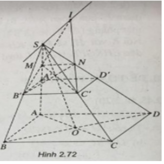
a) (P) // BC nên (P) sẽ cắt (SBC) theo giao tuyến B'C' song song với BC.
Tương tự, (P) cắt (SAD) theo giao tuyến MN song song với AD.
Khi M trùng với trung điểm A' của cạnh SA thì thiết diện MB'C'N' là hình bình hành.
b) Với M không trùng với A':
Gọi I ∈ B′M ∩ C′N. Ta có:
I ∈ B′M ⊂ (SAB), tương tự I′ ∈ C′N ⊂ (SCD)
Như vậy I ∈ Δ = (SAB) ∩ (SCD).

Gọi (P) là mặt phẳng qua M, song song DE và SC
Gọi O là giao điểm AC, BD \(\Rightarrow\) O là trung điểm AC
\(\Rightarrow\) OM là đường trung bình tam giác SAC
\(\Rightarrow OM||SC\Rightarrow O\in\left(P\right)\)
Trong mp (SBD), gọi F là trung điểm BE \(\Rightarrow OF\) là đường trung bình tam giác BDE
\(\Rightarrow OF||DE\Rightarrow F\in\left(P\right)\)
Trong mp (SBC), qua F kẻ đường thẳng song song SC cắt BC tại G
\(\Rightarrow G\in\left(P\right)\)
Trong mp (ABCD), nối GO kéo dài cắt AD tại H
\(\Rightarrow H\in\left(P\right)\)
\(\Rightarrow\) Thiết diện của (P) và chóp là tứ giác MFGH (và tứ giác này không có điều gì đặc biệt)