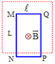
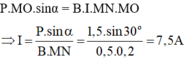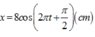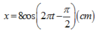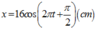Trong một từ trường đều có \(\overrightarrow{B}\) thẳng đứng, cho một dòng các ion bắt đầu đi vào từ trường từ điểm A và đi ra điểm C, sao cho AC là \(\frac{1}{2}\) đường tròn trong mặt phẳng ngang. Các ion có cùng điện tích, cùng vận tốc ban đầu. Cho biết khoảng cách AC giữa điểm đi vào và điểm đi ra đối với ion C2H5OH+ là 22,5 cm, xác định khoẳng cách AC đối với các ion C2H5OH+; C2H5+; OH+; CH2OH+; CH3+; CH2+.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trong từ trường đều B, ion C2H5O+ (m1 = 45đvC) chuyển động tròn với bán kính R1.
Ta có: 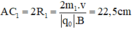
- Đối với ion C2H5OH (m2 = 46đvC)
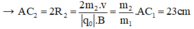
- Đối với ion C2H5+ (m3 = 29đvC)
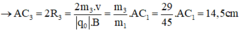
- Đối với ion OH+ (m4 = 17đvC)
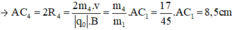
- Đối với ion CH2OH+ (m5 = 31đvC)
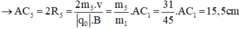
- Đối với ion CH3+ (m6 = 15đvC)
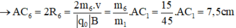
- Đối với ion CH2+ (m7 = 14đvC)
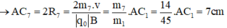

Đáp án D
Phương pháp: Sử dụng lí thuyết về phương trình dao động điều hoà
Cách giải:
Biên độ dao động: A = 8cm
Ta có: v = ωA=16π cm/s =>ω = 2π (rad/s)
Chất điểm bắt đầu đi từ vị trí thấp nhất của đường tròn, vậy pha ban đầu là φ = –π/2 (rad)
=> x = 8 cos 2 πt - π 2

Đáp án C
Phương pháp: Xác định A, ω và φ của phương trình x = Acos(ωt + φ)
Sử dụng mối liên hệ giữa dao động điều hoà và chuyển động tròn đều.
Cách giải:
+ Biên độ dao động: A = R = 8cm
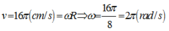
+ Tốc độ:
+ Chất điểm bắt đầu từ vị trí thấp nhất của đường tròn theo chiều ngược chiều kim đồng hồ:
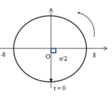
= Pha ban đầu: φ = -π/2
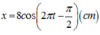
= Phương trình:

Chọn đáp án C.
+ Biên độ dao động: A = R = 8cm
![]()
![]()
+ Tốc độ:
+ Chất điểm bắt đầu từ vị trí thấp nhất của đường tròn theo chiều ngược chiều kim đồng hồ:

= Pha ban đầu: φ = -π/2
![]()
= Phương trình:

Đáp án: A
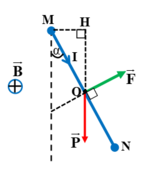
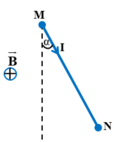
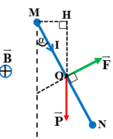
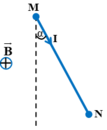
Thanh chịu tác dụng của hai lực: Trọng lực P → , lực từ F →
Điều kiện cân bằng của thanh MN: P. MH = F. MO
Suy ra: