Tìm đa thức dư của đa thức x2015-x10-x8 chia cho đa thức x2-1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án C
Phương pháp: Áp dụng công thức khai triển tổng quát: a + b n = ∑ k = 0 n C n k . a n − k . b k . Đối với bài toán này ta áp dụng công thức 1 + x n = ∑ k = 0 n C n k .1 n − k . x k . Sau đó dựa vào khai triền bài toán cho P x = a 0 + a 1 x + a 2 x 2 + ... + a 2 x 12 ta tìm được hệ số a 8 (đi theo x 8 )
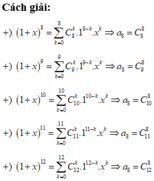
Vậy Hệ số cần tìm là a 8 = C 8 8 + C 9 8 + C 10 8 + C 11 8 + C 12 8 = 1 + 9 + 45 + 165 + 495 = 715

Đáp án D
a 8 = C 8 8 + C 9 8 + C 10 8 + C 11 8 + C 12 8 = 1 + 9 + 45 + 165 + 495 = 715


Do đa thức chia có bậc 2
nên đa thức dư là nhị thức bậc nhất
Đặt đa thức dư là \(ax+b\)
Đa thức thương là \(Q_{\left(x\right)}\)
\(\Rightarrow x+x^5+x^{10}+x^{20}=\left(x^2-1\right)Q_{\left(x\right)}+ax+b\\ \Leftrightarrow\left(x+1\right)\left(x-1\right)Q_{\left(x\right)}+ax+b\)
Đẳng thức trên luôn đúng \(\forall x\)
nên lần lượt cho \(x=1;x=-1\)
\(\text{Ta được : }\left\{{}\begin{matrix}a+b=4\\b-a=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=\dfrac{4-0}{2}\\b=\dfrac{4+0}{2}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=2\\b=2\end{matrix}\right.\)
\(\Rightarrow ax+b=2x+2\)
Vậy số dư trong phép chia \(f_{\left(x\right)};g_{\left(x\right)}\)
là \(2x+2\)

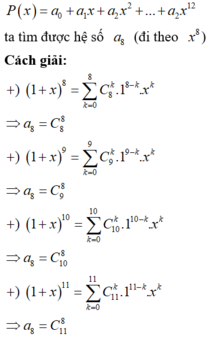
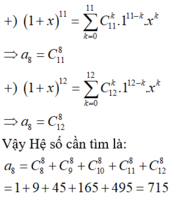


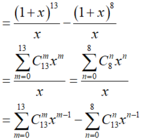
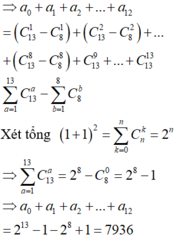
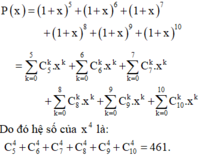
Bậc của đa thức chia x2 - 1 bằng 2 => Đa thức dư có dạng ax + b. Gọi Q(x) là thương của phép chia
=> x2015 - x10 - x8 = (x2 - 1).Q(x) + (ax + b)
Thay lần lượt x = 1; x = -1 ta được:
-1 = a + b
-3 = -a + b
=> (a+ b) + (-a + b) = 2b = -4 => b = - 2 => a = -1 - (-2) = 1
Vậy đa thức dư là: x - 2