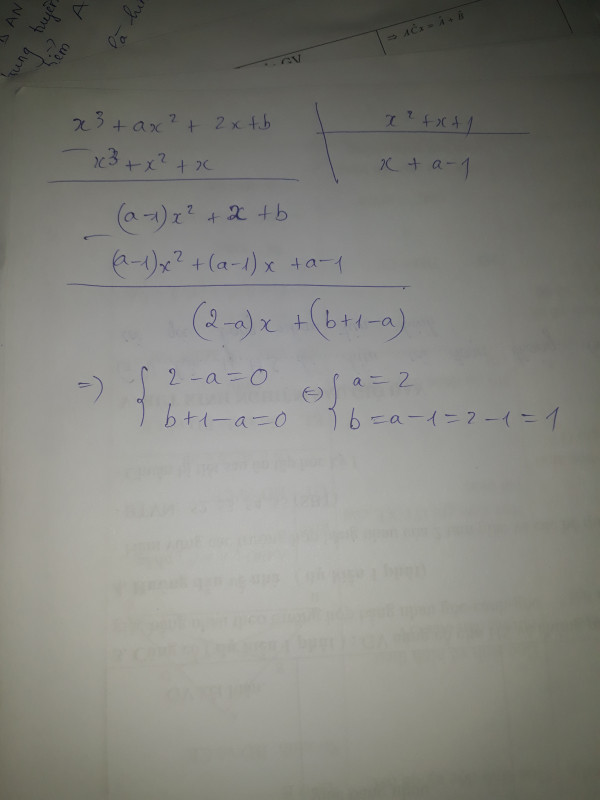Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(f\left(x\right)=x^3+2ax+b\)
Vì \(f\left(x\right)⋮\left(x-1\right)\)\(\Rightarrow f\left(1\right)=0\)\(\Leftrightarrow1+2a+b=0\)\(\Leftrightarrow2a+b=-1\)(1)
Vì \(f\left(x\right)\)chia \(x+2\)dư \(3\) \(\Rightarrow f\left(-2\right)=3\)
\(\Leftrightarrow-8-4a+b=3\Leftrightarrow-4a+b=11\Leftrightarrow4a-b=-11\)(2)
Cộng (1) với (2) ta được \(2a+b+4a-b=6a=-1-11=-12\)\(\Rightarrow a=-2\)
\(\Rightarrow b=3\)
Vậy \(a=-2;b=3\)

Lời giải:
Đặt $f(x)=x^3+2ax+b$
Áp dụng định lý Bê-du về phép chia đa thức, ta có:
\(\left\{\begin{matrix} f(1)=1+2a+b=0\\ f(-2)=(-2)^3+2a(-2)+b=3\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 2a+b=-1\\ -4a+b=11\end{matrix}\right.\)
\(\Rightarrow \left\{\begin{matrix} a=-2\\ b=3\end{matrix}\right.\)
Vậy.......

2x^3+3x^2-x+a x^2+x-1 2x+1 2x^3+x^2 - - 2x^2-x+a 2x^2+x -2x+a -2x-1 - a+1
Để \(A\left(x\right)⋮B\left(x\right)\Leftrightarrow a+1=0\)
\(\Leftrightarrow a=-1\)
Vậy ...

Bài 1 : Đa thức chia là bậc 2 do đó đa thức dư nhiều nhất sẽ là bậc 1 .
Ta có : \(P\left(x\right)=Q\left(x\right).\left(x^2-5x+6\right)+ax+b\)
Theo bài ra ta có hệ phương trình :
\(\left\{{}\begin{matrix}P\left(2\right)=2a+b=-2\\P\left(3\right)=3a+b=-3\end{matrix}\right.\)
Giải hệ phương trình ta tìm được :
\(\left\{{}\begin{matrix}a=-1\\b=0\end{matrix}\right.\)
Vậy số dư trong phéo chia là \(-x\)
Bài 2 : Mình suy nghĩ sau !
Chúc bạn học tốt

a) \(x^3+x^2-x+a=\left(x^2-x+1\right)\left(x+2\right)+\left(a-2\right)\).
Đa thức trên chia hết cho \(x+2\) khi và chỉ khi a = 2.
b) \(x^3+ax^2+2x+b=\left(x^2+x+1\right)\left(x+1\right)+\left(a-2\right)x^2+\left(b-1\right)\) chia hết cho \(x^2+x+1\) khi và chỉ khi:
\(\frac{a-2}{1}=\frac{0}{1}=\frac{b-1}{1}\Leftrightarrow a=2;b=1\).
c) Tương tự.

Gọi r(x) = ax + b là dư trong phép chia f(x) cho (x-1)(x-2)
Theo đề bài ta có :
f(x) = (x-1).A(x) + 2 [ A(x) là thương trong phép chia f(x) cho (x-1) ](1)
f(x) = (x+2).B(x) + 4 [ B(x) ___________________________ (x+2) ](2)
f(x) = (x-1)(x-2).C(x) + ax + b [ C(x) ___________________ (x-1)(x+2) ](3)
Với x = 1 ta có \(\hept{\begin{cases}\left(1\right)=2\\\left(3\right)=a+b\end{cases}}\Rightarrow a+b=2\)(*)
Với x = -2 ta có \(\hept{\begin{cases}\left(2\right)=4\\\left(3\right)=-2a+b\end{cases}}\Rightarrow-2a+b=4\)(**)
Từ (*) và (**) \(\Rightarrow\hept{\begin{cases}a+b=2\\-2a+b=4\end{cases}}\Leftrightarrow\hept{\begin{cases}3a=-2\\a+b=2\end{cases}}\Leftrightarrow\hept{\begin{cases}a=-\frac{2}{3}\\b=\frac{8}{3}\end{cases}}\)
Vậy dư là -2/3x + 8/3