Tính B = x19-5x18+5x17-5x16+......- 5x2+5x +1886 với x=4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


x = 4 => 5 = x + 1 thay vào ta có:
x^19 - (x+1).x^18+....+(x+1)x + 1886
= x^ 19 - x^19 +x^18 +...+x^2 + x +1886 = x +1886 = 4 + 1886 = 1890
Ấn đúng hộ tơ nhe

\(a,\frac{2}{5}:\frac{6}{5}+\frac{3}{4}.\frac{12}{5}\)
=\(\frac{2}{5}.\frac{5}{6}+\frac{9}{5}\)
=\(\frac{1}{3}+\frac{9}{5}\)
=\(\frac{32}{5}\)
b) \(\frac{17}{5}.\frac{3}{5}.\frac{17}{5}.\frac{2}{5}\)
=\(\frac{17}{5}.\left(\frac{3}{5}.\frac{2}{5}\right)\)
=\(\frac{17}{5}.\frac{6}{25}\)
=\(\frac{102}{125}\)
c)\(\frac{1}{4}+\frac{3}{4}.\frac{2}{3}-\frac{1}{2}\)
=\(\frac{1}{4}+\frac{1}{2}-\frac{1}{2}\)
=\(\frac{1}{4}\)
d)\(\frac{6}{7}+\frac{5}{8}:5\)
=\(\frac{6}{7}+\frac{5}{8}.\frac{1}{5}\)
=\(\frac{6}{7}+\frac{1}{8}\)
=\(\frac{48}{56}+\frac{7}{56}\)
=\(\frac{55}{56}\)
tk nhé bn!

a: =-29x100=-2900
b: \(=\left(215-5\cdot80+5\cdot50+60\right):53=\dfrac{125}{53}\)

a: =-29x(165-65)=-29x100=-2900
b: \(=\left[215-5\cdot30-60\right]:53=0\)

Bài 2:
\(a,\Leftrightarrow x^5-x^3+5x+a=\left(x+1\right)\cdot a\left(x\right)\)
Thay \(x=-1\Leftrightarrow-1+1-5+a=0\Leftrightarrow a=5\)
\(b,\Leftrightarrow x^4+x^3+ax-2=\left(x-2\right)\cdot b\left(x\right)\)
Thay \(x=2\Leftrightarrow16+8+2a-2=0\Leftrightarrow2a=-22\Leftrightarrow a=-11\)
Bài 1:
\(x^{19}-x-3=\left(x+1\right)\cdot a\left(x\right)+R\) với R là hằng số (do x+1 bậc 1)
Thay \(x=-1\Leftrightarrow-1+1-3=R\Leftrightarrow R=-3\)
Vậy phép chia dư -3

\(a,=15x^4-12x^3+9x^2\\ b,=-15x^3y^2+25x^2y^2-5xy^3\\ c,=5x^3-19x^2+12x\\ d,=3x^3+xy^2+5x^2y-9x^2y-3y^3-15xy^2\\ =3x^3-3y^3-14xy^2-4x^2y\)

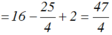
Thay \(5=x+1\) vào biểu thức B ,có :
\(x^{19}-\left(x+1\right)x^{18}+\left(x+1\right)x^{17}-\left(x+1\right)x^{16}+...-\left(x+1\right)x^2+\left(x+1\right)x+1886\)
\(=x^{19}-x^{19}-x^{18}+x^{18}+x^{17}-x^{17}+x^{16}+...-x^3-x^2+x^2+x+1886\)
\(=x+1886\)
\(=4+1886\)
\(=1890\)
Vậy tại x = 4 giá trị của biểu thức B là 1890
\(\text{Ta có : }x=4\Rightarrow\left\{{}\begin{matrix}x+1\\-x+1890\end{matrix}\right.\\ \Rightarrow B=x^{19}-5x^{18}+5x^{17}-...-5x^2+5x+1886\\ =x^{19}-\left(x+1\right)x^{18}+\left(x+1\right)x^{17}-...-\left(x+1\right)x^2+\left(x+1\right)x-x+1890\\ =x^{19}-x^{19}-x^{18}+x^{18}+x^{17}-...-x^3-x^2+x^2+x-x+1890\\ \\=1890\)