Giải thích chi tiết ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1 D => doesn't (ở vế đầu dùng động từ thường nên sau but cũng phải dùng động từ nhưng phủ định nên dùng trợ động từ)
2 D => at (arrived at + địa điểm cụ thể)
3 A => to playing (in addition to + Ving)
4 C => the piano (chơi nhạc cụ thì dùng the phía trc nhạc cụ đó)
5 A => careless-prepared (dịch nghĩa)

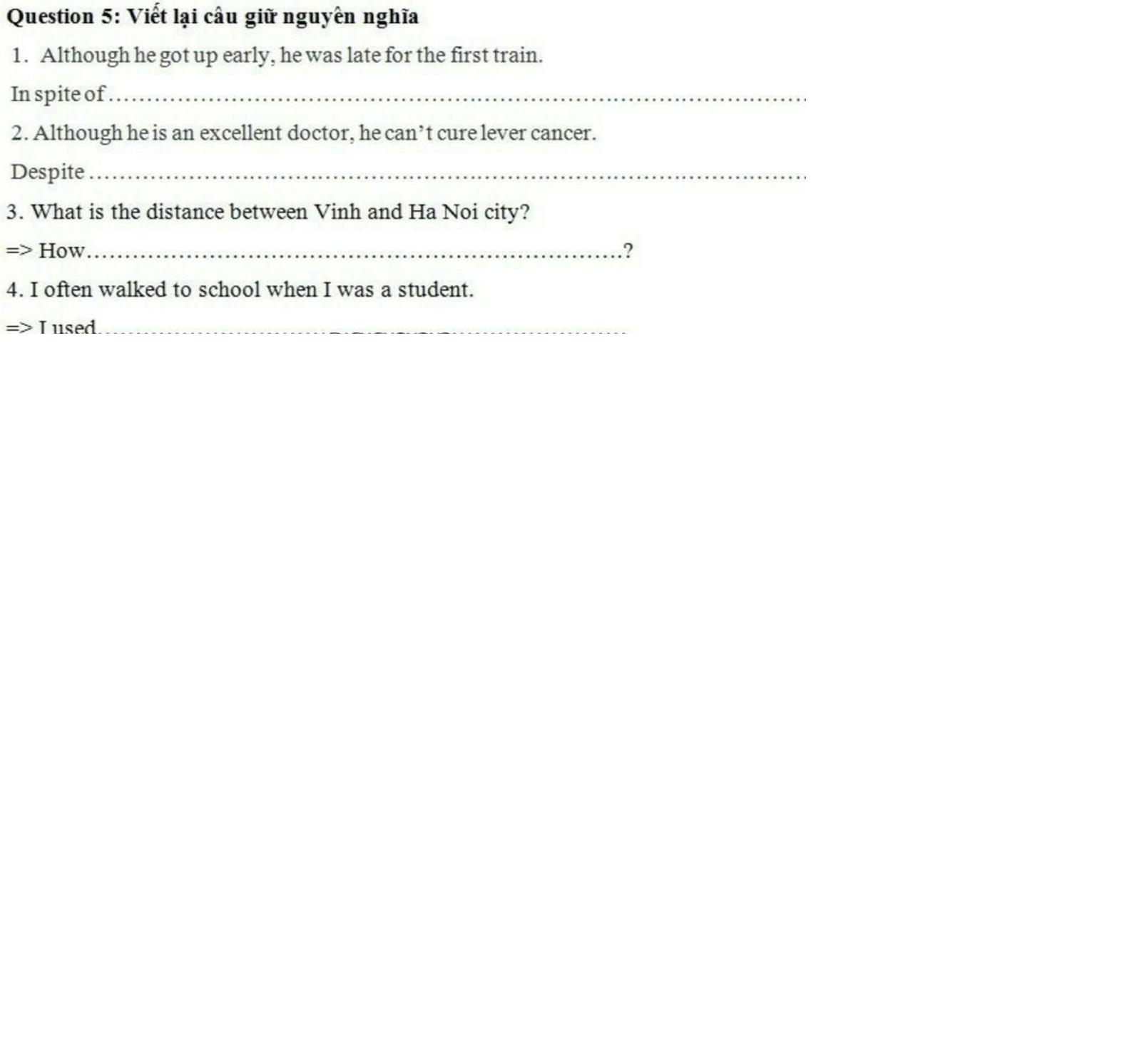
1. In spite of getting up early, he was late for the first train (Cấu trúc In spite of +V-ing)
2. Despite being an excellent doctor, he can’t cure lever cancer. (cấu trúc despite+ving)
3. How far is it from Vinh to HN?
4. I used to walk to school when I was small (cấu trúc used to+ to V)

1 wash (made sb Vo)
2 cleaned (had st + V3)
3 cashed(had st + V3)
4 to go (ask sb to V)
5 stay (made sb Vo)
6 painted (had st + V3)
7 to write (told sb to V)
8 shortened (had st + V3)
9 redo (made sb Vo)
10 filled (had st + V3)

1 B đọc là t∫ən còn lại là ∫n
2 A đọc là iz còn lại là ik
3 C đọc là ou còn lại là ə
4 B đọc là æ còn lại là ə
5 C đọc i: còn lại là i
6 D đọc là z còn lại lá
7 B đọc là i còn lại là ai
8 C đọc là ə còn lại là ʌ
9 C đọc dài hơn
10 A là i còn lại là e

Thứ tự sắp xếp các cụm từ: \(\left(1\right);\left(3\right);\left(2\right);\left(4\right)\)

Bài 1:
a) \(\dfrac{7}{8}>\dfrac{11}{13}\)
b) \(\dfrac{2010}{2011}< \dfrac{2011}{2012}\)
c) \(-\dfrac{17}{16}< -\dfrac{2}{3}\)
d) \(-\dfrac{2010}{2011}< \dfrac{2011}{-2000}\)


 giải thích chi tiết với ạ
giải thích chi tiết với ạ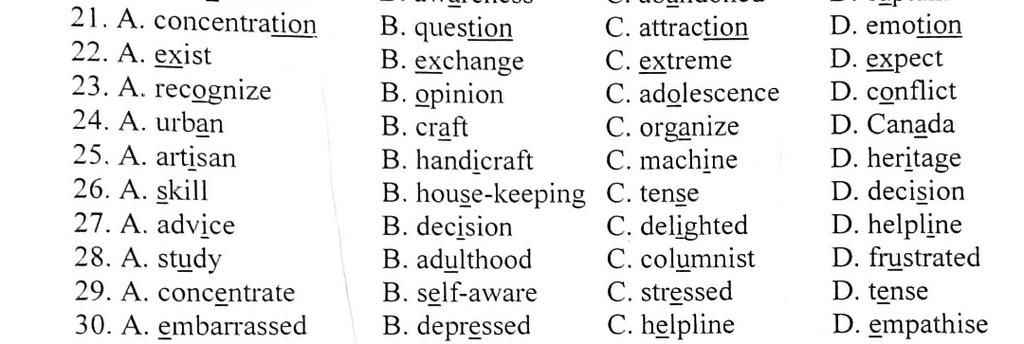 GIẢI THÍCH CHI TIẾT GIÚP E Ạ
GIẢI THÍCH CHI TIẾT GIÚP E Ạ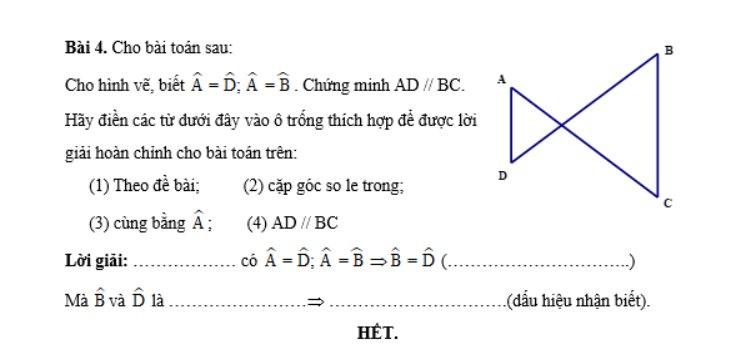
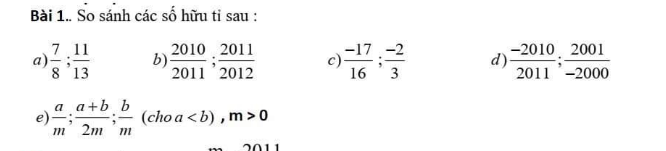
\(c,x\left(\dfrac{1}{5}+\dfrac{1}{4}\right)-\left(\dfrac{1}{7}+\dfrac{1}{8}\right)=0\\ \Leftrightarrow\dfrac{9}{20}x-\dfrac{15}{56}=0\\ \Leftrightarrow x=\dfrac{15}{56}\cdot\dfrac{20}{9}=\dfrac{25}{42}\)
\(d,\left(2x-\dfrac{2}{3}\right)\left(x+0,5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{2}{3}\\x=-\dfrac{1}{2}\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=-\dfrac{1}{2}\end{matrix}\right.\)
\(4,\)
\(\left(-111\right):\left(-\dfrac{1}{11}\right)=1221\)
d: Ta có: \(\left(2x-\dfrac{2}{3}\right)\left(x+\dfrac{1}{2}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{2}{3}\\x=-\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=-\dfrac{1}{2}\end{matrix}\right.\)