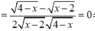\(\text{Gía trị lớn nhất của hàm số: }y=2\sqrt{1+x}+\sqrt{3-x}-\sqrt{-x^2+2x+3}\text{đạt tại }x_0=?\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
PD
1

AH
Akai Haruma
Giáo viên
28 tháng 8 2021
Lời giải:
Đặt $\sqrt[3]{1-x}=a; \sqrt[4]{1+x}=b$ thì bài toán trở thành:
Cho $a,b\geq 0$ thỏa mãn $a^4+b^4=2$
Tìm max $P=ab+a+b$
Thật vậy, áp dụng BĐT AM-GM:
$2=a^4+b^4\geq 2a^2b^2\Rightarrow ab\leq 1$
$a^4+b^4\geq \frac{1}{2}(a^2+b^2)^2$
$a^2+b^2\geq \frac{1}{2}(a+b)^2$
$\Rightarrow 2=a^4+b^4\geq \frac{(a+b)^4}{8}$
$\Rightarrow (a+b)^4\leq 16$
$\Rightarrow a+b\leq 2$
Do đó: $P=ab+a+b\leq 1+2=3$
Vậy $P_{\max}=3$ khi $a=b=1\Leftrightarrow x=0$

NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 3 2021
\(\sqrt{4-x}\ge0\) với mọi x thuộc TXĐ nên \(y=\sqrt{4-x}+\sqrt{3}\ge\sqrt{3}\)
Đáp án D
PT
1