Cho hình vẽ, biết Ax // Dy. Chứng minh: OB vuông góc với OC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 5
A B C D E y x
\(\widehat{A}+\widehat{D}=180^o\) (Hai góc trong cùng phía bù nhau)
\(\widehat{DAx}=\widehat{BAx}=\dfrac{\widehat{A}}{2}\) (gt)
\(\widehat{ADy}+\widehat{CDy}=\dfrac{\widehat{D}}{2}\) (gt)
\(\Rightarrow\widehat{DAx}+\widehat{ADy}=\dfrac{\widehat{A}}{2}+\dfrac{\widehat{D}}{2}=\dfrac{180^o}{2}=90^o\)
Xét tg ADE có
\(\widehat{AED}=180^o-\left(\widehat{DAx}+\widehat{ADy}\right)=180^o-90^o=90^o\) (Tổng các góc trong của tg bằng 180 độ)
\(\Rightarrow Ax\perp Dy\)
Bài 6:
A B C E D
a/
Ta có
AB//CD => AB//DE
BE//AB (gt)
=> ABED là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
=> AB = DE; AD = BE (Trong hình bình hành các cạnh đối nhau thì bằng nhau)
b/
CD - DE = CE
Mà AB = DE (cmt)
=> CD - AB = CE
c/
Xét tg BCE có
BC+BE>CE (trong tg tổng độ dài 2 cạnh lớn hơn độ dài cạnh còn lại)
Mà CE = CD - DE và DE = AB (cmt) và BE = AD
=> BC+BE = BC + AD>CE = CD - AB
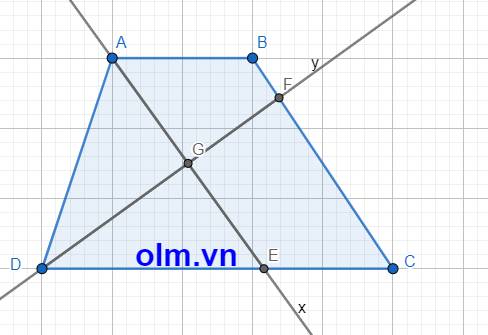
Gọi G là giao điểm của hai đường phân giác Ax và By
Ta có: \(\widehat{ADG}\) = \(\dfrac{1}{2}\)\(\widehat{ADE}\) ( vì DG là phân giác góc ADE)
\(\widehat{DAG}\) = \(\dfrac{1}{2}\)\(\widehat{DAB}\)( vì AG là phân giác góc DAB )
⇒ \(\widehat{ADG}\) + \(\widehat{DAG}\) = \(\dfrac{1}{2}\)\(\widehat{ADE}\) + \(\dfrac{1}{2}\)\(\widehat{DAB}\) = \(\dfrac{1}{2}\)(\(\widehat{ADE}\) + \(\widehat{DAB}\))
\(\widehat{ADE}\) + \(\widehat{DAB}\) = 1800 (vì hai góc là hai góc trong cùng phía)
⇒ \(\widehat{ADG}\) + \(\widehat{DAG}\) = \(\dfrac{1}{2}\) \(\times\) 1800 = 900
Xét tam giác ADG có: \(\widehat{GAD}\) + \(\widehat{ADG}\) + \(\widehat{DGA}\) = 1800 (tổng ba góc trong 1 tam giác bằng 1800)
⇒ \(\widehat{DGA}\) = 1800 - 900 = 900
Vậy tam giác ADG vuông tại G ⇒AE \(\perp\) DG (đpcm)

Bài giải
A B C D x y 1 1 O
Trong hình thang ABCD có : \(AB\text{ }//\text{ }CD\text{ }\Rightarrow\text{ }\widehat{A}\text{ và }\widehat{D}\text{ là hai góc trong cùng phía }\)
\(\Rightarrow\text{ }\widehat{A}+\widehat{D}=180^o\text{ }\Rightarrow\text{ }\frac{1}{2}\widehat{A}+\frac{1}{2}\widehat{D}=\frac{1}{2}\cdot180^o\text{ }\Rightarrow\text{ }\widehat{A_1}+\widehat{D_1}=90^o\)
Trong \(\Delta AOD\) có : \(\widehat{A_1}+\widehat{O}+\widehat{D_1}=180^o\) Mà \(\text{ }\widehat{A_1}+\widehat{D_1}=90^o\text{ }\Rightarrow\text{ }\widehat{O}=90^o\)
\(\Rightarrow\text{ }Ax\text{ }\perp\text{ }Dx\text{ ( }ĐPCM\text{ )}\)

30 30 x y A B C
a,Do \(\widehat{yOB}\)<\(\widehat{yOx}\)và tia OB nằm trong góc \(\widehat{xOy}\)
\(\Rightarrow\)Tia OB nằm giữa hai tia Ox,Oy
\(\Rightarrow\)\(\Rightarrow\widehat{yOB}\)+\(\widehat{BOx}\)=\(\widehat{xOy}\)
\(\Rightarrow30^o+\widehat{BOx}\)\(=90^o\)
\(\Rightarrow\widehat{BOx}\)\(=60^o\)
Do \(\widehat{xOA}\)<\(\widehat{xOB}\)và hai tia OA,OB cùng nằm trong \(\widehat{xOy}\)
\(\Rightarrow\widehat{xOA}+\widehat{AOB}=\widehat{xOB}\)
\(\Rightarrow30^o+\widehat{AOB}=60^o\)
\(\Rightarrow\widehat{AOB}=30^o\)
Do \(\widehat{xOA}=\widehat{AOB}\)\(=\frac{\widehat{BOx}}{2}=\frac{60^o}{2}=30^o\)
\(\Rightarrow\)Tia OA là tia phân giác của \(\widehat{xOB}\)
b, mk chịu

Kéo dài BO cắt Dy tại N
\(\Rightarrow\widehat{ABN}=\widehat{BNC}=60^o\) (góc so le trong)
Xét tg ONC có
\(\widehat{NOC}=180^o-\left(\widehat{BNC}+\widehat{OCN}\right)=180^o-\left(60^o+30^o\right)=90^o\Rightarrow OB\perp OC\)