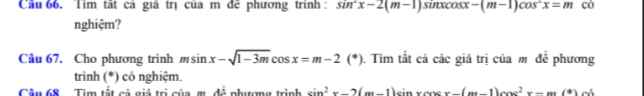Giải giúp e câu 22 vs ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


sinx - sin3x - \(\sqrt{3}\left(cosx+sin3x\right)=0\)
⇔ sinx - \(\sqrt{3}cosx-\left(1+\sqrt{3}\right)sin3x\) = 0
⇔ \(2sin\left(x-\dfrac{\pi}{3}\right)-\left(1-\sqrt{3}\right)sin\left(\pi-3x\right)\) = 0
⇔ \(2sin\left(x-\dfrac{\pi}{3}\right)+\left(1-\sqrt{3}\right)sin\left(3x-\pi\right)=0\)
⇔ \(2sin\left(x-\dfrac{\pi}{3}\right)+\left(1-\sqrt{3}\right)sin3\left(x-\dfrac{\pi}{3}\right)=0\)
Đặt a = x - \(\dfrac{\pi}{3}\) ta có phương trình mới
2sina + (1 - \(\sqrt{3}\))sin3a = 0 (1)
Sử dụng công thức sin3a = 3sina - 4sin3a đưa (1) về phương trình bậc 3 ẩn là a. Từ a suy ra x





Câu 84:
$\sin 3x+2\cos ^2x=1$
$\sin 3x=1-2\cos ^2x=-\cos 2x=\sin (2x-\frac{\pi}{2})$
\(\Rightarrow \left[\begin{matrix} 3x=2x-\frac{\pi}{2}+2k\pi\\ 3x=\frac{3}{2}\pi-2x+2k\pi\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=(2k+\frac{3}{2})\pi\\ x=\frac{2k+\frac{3}{2}}{5}\pi\end{matrix}\right.\) với $k$ nguyên
Nghiệm âm lớn nhất của pt:
$x=\frac{2(-1)+\frac{3}{2}}{5}\pi =\frac{-\pi}{10}$
84.
\(sin3x+2cos^2x=1\)
\(\Leftrightarrow sin3x+cos2x=0\)
\(\Leftrightarrow cos\left(\dfrac{\pi}{2}-3x\right)+cos2x=0\)
\(\Leftrightarrow2cos\left(\dfrac{\pi}{4}-\dfrac{x}{2}\right).cos\left(\dfrac{\pi}{4}-\dfrac{5x}{2}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos\left(\dfrac{\pi}{4}-\dfrac{x}{2}\right)=0\\cos\left(\dfrac{\pi}{4}-\dfrac{5x}{2}\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{\pi}{4}-\dfrac{x}{2}=\dfrac{\pi}{2}+k\pi\\\dfrac{\pi}{4}-\dfrac{5x}{2}=\dfrac{\pi}{2}+k\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{2}-k2\pi\\x=-\dfrac{\pi}{10}-\dfrac{k2\pi}{5}\end{matrix}\right.\)
\(x=-\dfrac{\pi}{2}-k2\pi< 0\Leftrightarrow k>-\dfrac{1}{4}\Rightarrow k=0\Rightarrow x=-\dfrac{\pi}{2}\)
\(x=-\dfrac{\pi}{10}-k2\pi< 0\Leftrightarrow k>-\dfrac{1}{20}\Rightarrow k=0\Rightarrow x=-\dfrac{\pi}{10}\)
Vậy \(x=-\dfrac{\pi}{10}\) là nghiệm âm lớn nhất

ĐKXĐ: \(1-3m\ge0\Rightarrow m\le\dfrac{1}{3}\) (1)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất:
\(m^2+\left(1-3m\right)\ge\left(m-2\right)^2\)
\(\Leftrightarrow1-3m\ge-4m+4\Rightarrow m\ge3\) (2)
Kết hợp (1); (2) \(\Rightarrow\) không tồn tại m thỏa mãn


Câu 19 : Phép đối xứng qua tâm M biến đường tròn (O;R) thành đường tròn (O' ; R)
=> Đường tròn này cố định
H thuộc đường tròn này đấy. CM thì dùng Kiến thức lớp 9 ấy. Thế nhá
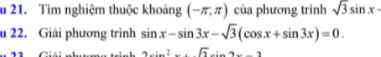



 giải giúp e câu 2,4,5,6 vs ạ.
giải giúp e câu 2,4,5,6 vs ạ.