K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 4 2022
21.
Giới hạn đã cho hữu hạn khi và chỉ khi \(a=1\)
Khi đó:
\(\lim\limits_{x\rightarrow+\infty}\left(x-\sqrt{x^2+bx+2}\right)=\lim\limits_{x\rightarrow+\infty}\dfrac{x^2-\left(x^2+bx+2\right)}{x+\sqrt{x^2+bx+2}}=\lim\limits_{x\rightarrow+\infty}\dfrac{-bx-2}{x+\sqrt{x^2+bx+2}}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{-b-\dfrac{2}{x}}{1+\sqrt{1+\dfrac{b}{x}+\dfrac{2}{x^2}}}=\dfrac{-b}{2}\)
\(\Rightarrow-\dfrac{b}{2}=4\Rightarrow b=-8\)
\(\Rightarrow a+b=1-8=-7\)
22.
B sai, do các cạnh bên của chóp đều tạo với đáy các góc bằng nhau
NT
5
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 10 2021
b.
\(\Leftrightarrow\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=-\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=-\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{3}=\dfrac{2\pi}{3}+k2\pi\\x+\dfrac{\pi}{3}=-\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=-\pi+k2\pi\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 10 2021
c.
\(\Leftrightarrow\dfrac{3}{5}sinx-\dfrac{4}{5}cosx=1\)
Đặt \(\dfrac{3}{5}=cosa\) với \(a\in\left(0;\dfrac{\pi}{2}\right)\Rightarrow\dfrac{4}{5}=sina\)
Pt trở thành:
\(sinx.cosa-cosx.sina=1\)
\(\Leftrightarrow sin\left(x-a\right)=1\)
\(\Leftrightarrow x-a=\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=a+\dfrac{\pi}{2}+k2\pi\)
KB
3 tháng 5 2022
\(y=tan\left(\sqrt{x^2+4}\right)\Rightarrow y'=\dfrac{1}{cos^2\left(\sqrt{x^2+4}\right)}.\left(\sqrt{x^2+4}\right)'\)
\(\left(\sqrt{x^2+4}\right)'=\dfrac{1}{2\sqrt{x^2+4}}\left(x^2+4\right)'=\dfrac{2x}{2\sqrt{x^2+4}}=\dfrac{x}{\sqrt{x^2+4}}\)
Suy ra : \(y'=\dfrac{x}{cos^2\left(\sqrt{x^2+4}\right).\sqrt{x^2+4}}\)
HD
1
KB
1 tháng 5 2022
Ta có : \(f\left(2\right)=2a+b-6\)
\(\lim\limits_{x\rightarrow2^+}\dfrac{x-\sqrt{x+2}}{x^2-4}=\lim\limits_{x\rightarrow2^+}\dfrac{x^2-x-2}{\left(x-2\right)\left(x+2\right)\left(x+\sqrt{x+2}\right)}\)
\(=\lim\limits_{x\rightarrow2^+}\dfrac{x+1}{\left(x+2\right)\left(x+\sqrt{x+2}\right)}=\dfrac{3}{16}\)
\(\lim\limits_{x\rightarrow2^-}x^2+ax+3b=4+2a+3b\)
H/s liên tục tại điểm x = 2 \(\Leftrightarrow\dfrac{3}{16}=2a+3b+4=2a+b-6\)
Suy ra : \(a=\dfrac{179}{32};b=-5\) => t = a + b = 19/32 . Chọn C
TB
1
HP
23 tháng 9 2021
j, ĐK: \(x\ne\dfrac{\pi}{6}+\dfrac{k\pi}{2}\)
\(tan\left(\dfrac{\pi}{3}+x\right)-tan\left(\dfrac{\pi}{6}+2x\right)=0\)
\(\Leftrightarrow tan\left(\dfrac{\pi}{3}+x\right)=tan\left(\dfrac{\pi}{6}+2x\right)\)
\(\Leftrightarrow\dfrac{\pi}{3}+x=\dfrac{\pi}{6}+2x+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{6}+k\pi\left(l\right)\)
\(\Rightarrow\) vô nghiệm.
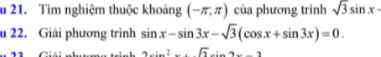
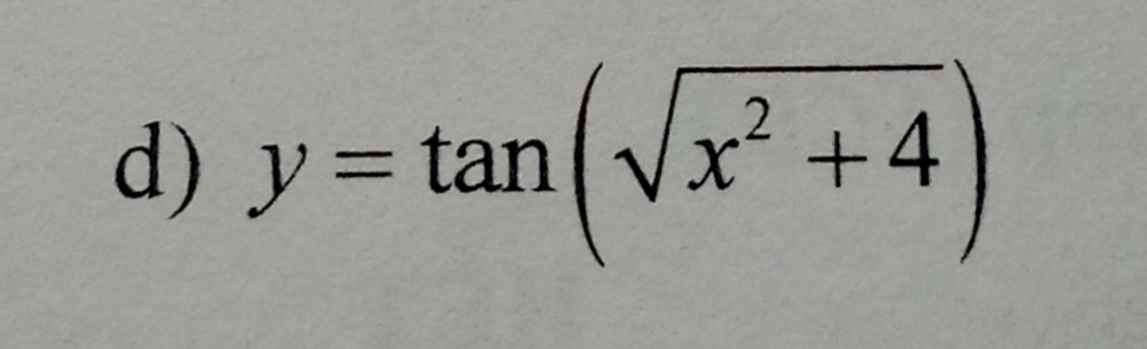
sinx - sin3x - \(\sqrt{3}\left(cosx+sin3x\right)=0\)
⇔ sinx - \(\sqrt{3}cosx-\left(1+\sqrt{3}\right)sin3x\) = 0
⇔ \(2sin\left(x-\dfrac{\pi}{3}\right)-\left(1-\sqrt{3}\right)sin\left(\pi-3x\right)\) = 0
⇔ \(2sin\left(x-\dfrac{\pi}{3}\right)+\left(1-\sqrt{3}\right)sin\left(3x-\pi\right)=0\)
⇔ \(2sin\left(x-\dfrac{\pi}{3}\right)+\left(1-\sqrt{3}\right)sin3\left(x-\dfrac{\pi}{3}\right)=0\)
Đặt a = x - \(\dfrac{\pi}{3}\) ta có phương trình mới
2sina + (1 - \(\sqrt{3}\))sin3a = 0 (1)
Sử dụng công thức sin3a = 3sina - 4sin3a đưa (1) về phương trình bậc 3 ẩn là a. Từ a suy ra x