làm giúp mình câu 10 và câu 11 ạ, mình đang cần gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 10:
a: Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}3x-8=-2x-3\\y=3x-8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\cdot1-8=-5\end{matrix}\right.\)
Thay x=1 và y=-5 vào (d3), ta được:
\(3m+2m+1=-5\)
hay \(m=-\dfrac{6}{5}\)

a: \(=\dfrac{2x+x-2-x-2}{\left(x-2\right)\left(x+2\right)}=\dfrac{2x-4}{\left(x-2\right)\left(x+2\right)}=\dfrac{2}{x+2}\)
b: x^2-x-6=0
=>(x-3)(x+2)=0
=>x=3(nhận) hoặc x=-2(loại)
Khi x=3 thì \(E=\dfrac{2}{3+2}=\dfrac{2}{5}\)
c: Để E nguyên thì \(x+2\in\left\{1;-1;2;-2\right\}\)
=>\(x\in\left\{-1;-3;0;-4\right\}\)

a: \(A=\left(x+2+2x-5\right)^2=\left(3x-3\right)^2\)
\(=\left(\dfrac{3}{4}-3\right)^2=\left(-\dfrac{9}{4}\right)^2=\dfrac{81}{16}\)

Câu 10:
$\sin ^2x=0\Leftrightarrow \sin x=0$
$\Rightarrow x=k\pi$ với $k$ nguyên.
Trong các khoảng đã cho chỉ có khoảng ở đáp án A chứa $k\pi$ với $k$ nguyên.
Câu 11:
PT\(\Leftrightarrow 2\sin x\cos x-\sin x-2+4\cos x=0\)
\(\Leftrightarrow 2\cos x(\sin x+2)-(\sin x+2)=0\)
\(\Leftrightarrow (2\cos x-1)(\sin x+2)=0\)
Vì $\sin x\geq -1$ nên $\sin x+2\geq 1>0$
$\Rightarrow 2\cos x-1=0$
$\Leftrightarrow \cos x=\frac{1}{2}=\cos \frac{\pi}{3}$
$\Rightarrow x=\frac{\pi}{3}+2k\pi$ hoặc $x=-\frac{\pi}{3} +2k\pi$ với $k$ nguyên.
Đáp án B.


10 C
11 A
12 D
13 B
14 D
15 D
16 B
17 A
18 C
19 D
20 B
21 B
22 C
23 A
24 A
25 C

Tất cả k dưới đây đều là \(k\in Z\)
6.
\(\Leftrightarrow\sqrt{3}cot\left(3x-\dfrac{\pi}{3}\right)=1\)
\(\Leftrightarrow cot\left(3x-\dfrac{\pi}{3}\right)=\dfrac{1}{\sqrt{3}}\)
\(\Leftrightarrow cot\left(3x-\dfrac{\pi}{3}\right)=cot\left(\dfrac{\pi}{3}\right)\)
\(\Leftrightarrow3x-\dfrac{\pi}{3}=\dfrac{\pi}{3}+k\pi\)
\(\Leftrightarrow3x=\dfrac{2\pi}{3}+k\pi\)
\(\Leftrightarrow x=\dfrac{2\pi}{9}+\dfrac{k\pi}{3}\)
7.
\(\Leftrightarrow\sqrt{3}tan\left(3x-15^0\right)=-1\)
\(\Leftrightarrow tan\left(3x-15^0\right)=-\dfrac{1}{\sqrt{3}}\)
\(\Leftrightarrow tan\left(3x-15^0\right)=tan\left(-30^0\right)\)
\(\Leftrightarrow3x-15^0=-30^0+k180^0\)
\(\Leftrightarrow3x=-15^0+k180^0\)
\(\Leftrightarrow x=-3^0+k60^0\)

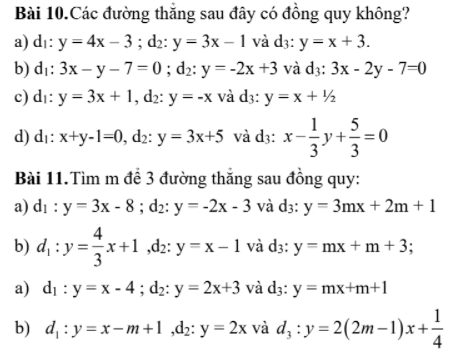







Bài 11:
a: Ta có: \(P=\dfrac{x^2-\sqrt{x}}{x+\sqrt{x}+1}\)
\(=\sqrt{x}\cdot\left(\sqrt{x}-1\right)\)
\(=x-\sqrt{x}\)
b: Để P=2 thì \(x-\sqrt{x}-2=0\)
hay x=4
Bài 10:
a: Ta có: \(A=\left(1+\dfrac{\sqrt{x}}{x+1}\right):\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{2\sqrt{x}}{x\sqrt{x}+\sqrt{x}-x-1}\right)\)
\(=\dfrac{x+\sqrt{x}+1}{x+1}:\dfrac{x-2\sqrt{x}+1}{\left(x+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x+\sqrt{x}+1}{x+1}\cdot\dfrac{x+1}{\sqrt{x}-1}\)
\(=\dfrac{x+\sqrt{x}+1}{\sqrt{x}-1}\)
b: Để A<0 thì \(\sqrt{x}-1< 0\)
hay x<1
Kết hợp ĐKXĐ, ta được: \(0\le x< 1\)
Để A=-1 thì \(x+\sqrt{x}+1=-\sqrt{x}+1\)
\(\Leftrightarrow x=0\)
c: Thay x=4 vào A, ta được:
\(A=\dfrac{4+2+1}{2-1}=7\)