Rút gọn:
3xn-2.(xn+2-yn+2)+yn+2.(3xn-2-yn-5) (n\(\varepsilon N;n\ge2\))
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Chọn A.
Ta có: 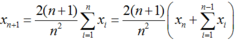
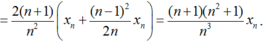
Do đó: 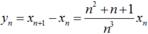
- Ta chứng minh dãy (yn) tăng.
Ta có: 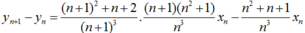
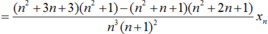
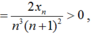
- Ta chứng minh dãy (yn) bị chặn.
Trước hết ta chứng minh: xn ≤ 4(n – 1) (1)
* Với n = 2, ta có: x2 = 4x1 = 4 nên (1) đúng với n = 2
* Giả sử (1) đúng với n, tức là: xn ≤ 4(n – 1), ta có
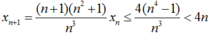
Nên (1) đúng với n + 1. Theo nguyên lí quy nạp ta suy ra (1) đúng
Ta có: 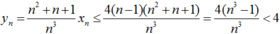
Vậy bài toán được chứng minh.



x(x – y) + y(x – y)
= x.x – x.y + y.x – y.y
= x2 – xy + xy – y2
= x2 – y2 + (xy – xy)
= x2 – y2
\(3x^{n-2}.\left(x^{n+2}-y^{n+2}\right)+y^{n+2}.\left(3x^{n-2}-y^{n-5}\right)\)
\(=3x^{n-2}.x^{n+2}-3x^{n-2}.y^{n+2}+y^{n+2}.3x^{n-2}-y^{n+2}.y^{n-5}\)
\(=3x^{2n}-\left(3xy\right)^{n-2}.y^4+\left(3xy\right)^{n-2}.y^4-y^{2n-3}\)
\(=3x^{2n}-y^{2n-3}\)
Chúc bạn học tốt!!!
\(\text{Ta có : }\)
\(\\ 3x^{n-2}\left(x^{n+2}-y^{n+2}\right)+y^{n+2}\left(3x^{n-2}-y^{n-5}\right)\)
\(\\ =3x^{n-2}\cdot x^{n+2}-3x^{n-2}\cdot y^{n+2}+y^{n+2}\cdot3x^{n-2}-y^{n+2}\cdot y^{n-5}\)
\(\\ =3x^{\left(n+2\right)+\left(n-2\right)}+\left(-3x^{n-2}\cdot y^{n+2}+y^{n+2}\cdot3x^{n-2}\right)-y^{\left(n+2\right)+\left(n-5\right)}\)
\(=3x^{n+2+n-2}-y^{n+2+n-5}\)
\(=3x^{\left(n+n\right)+\left(2-2\right)}-y^{\left(n+n\right)+\left(2-5\right)}\)
\(=3x^{2n}-y^{2n-3}\)