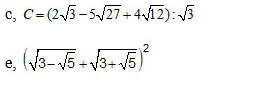
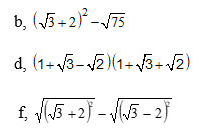 các bạn giải hộ mik mấy câu này vs mik đag cần gấp
các bạn giải hộ mik mấy câu này vs mik đag cần gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


29: Ta có: \(\dfrac{1}{\sqrt{7}+\sqrt{5}}+\dfrac{2}{1-\sqrt{7}}\)
\(=\dfrac{\sqrt{7}-\sqrt{5}}{2}-\dfrac{2\sqrt{7}-2}{6}\)
\(=\dfrac{3\sqrt{7}-3\sqrt{5}-2\sqrt{7}+2}{6}\)
\(=\dfrac{-3\sqrt{5}-2}{6}\)
30: Ta có: \(\dfrac{4}{1-\sqrt{3}}+\dfrac{\sqrt{3}-1}{\sqrt{3}+1}\)
\(=\dfrac{-4\sqrt{3}-4}{2}+\dfrac{4-2\sqrt{3}}{2}\)
\(=\dfrac{-4\sqrt{3}-4+4-2\sqrt{3}}{2}=-3\sqrt{3}\)
31: Ta có: \(\dfrac{1}{\sqrt{2}-\sqrt{3}}-\dfrac{3}{\sqrt{18}+2\sqrt{3}}\)
\(=-\sqrt{3}-\sqrt{2}-\dfrac{3}{3\sqrt{2}+2\sqrt{3}}\)
\(=-\sqrt{3}-\sqrt{2}-\dfrac{9\sqrt{2}-6\sqrt{3}}{6}\)
\(=\dfrac{-6\sqrt{3}-6\sqrt{2}-9\sqrt{2}+6\sqrt{3}}{6}=\dfrac{-15\sqrt{2}}{6}\)
\(=\dfrac{-5\sqrt{2}}{2}\)
29.
\(=\frac{\sqrt{7}-\sqrt{5}}{(\sqrt{7}-\sqrt{5})(\sqrt{7}+\sqrt{5})}+\frac{2(1+\sqrt{7})}{(1-\sqrt{7})(1+\sqrt{7})}\)
\(=\frac{\sqrt{7}-\sqrt{5}}{7-5}+\frac{2(1+\sqrt{7})}{1-7}=\frac{\sqrt{7}-\sqrt{5}}{2}-\frac{1+\sqrt{7}}{3}=\frac{\sqrt{7}-3\sqrt{5}-2}{6}\)

1: Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
=>CE\(\perp\)AB tại E
Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
=>BD\(\perp\)AC tại D
Xét ΔABC có
BD,CE là các đường cao
BD cắt CE tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC tại F
2: Xét ΔFBH vuông tại F và ΔFAC vuông tại F có
\(\widehat{FBH}=\widehat{FAC}\left(=90^0-\widehat{ACF}\right)\)
Do đó: ΔFBH~ΔFAC
=>\(\dfrac{FB}{FA}=\dfrac{FH}{FC}\)
=>\(FB\cdot FC=FA\cdot FH\)
3: Xét tứ giác AEHD có
\(\widehat{AEH}+\widehat{ADH}=90^0+90^0=180^0\)
nên AEHD là tứ giác nội tiếp đường tròn đường kính AH
Tâm I là trung điểm của AH

a.
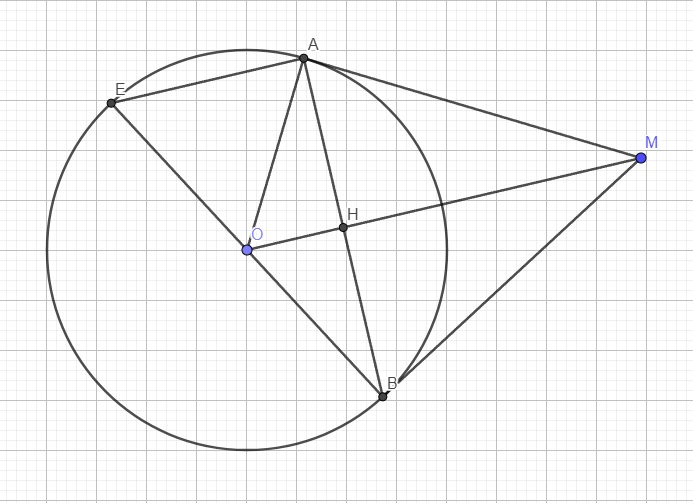
Do MA là tiếp tuyến tại A \(\Rightarrow MA\perp OA\Rightarrow\widehat{MAO}=90^0\)
Xét hai tam giác OMA và OMB có:
\(\left\{{}\begin{matrix}OA=OB=R\\MA=MB\left(gt\right)\\OM\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta OMA=\Delta OMB\left(c.c.c\right)\)
\(\Rightarrow\widehat{MBO}=\widehat{MAO}=90^0\)
\(\Rightarrow MB\perp OB\Rightarrow MB\) là tiếp tuyến
b.
Gọi H là giao điểm AB và OM
Ta có: \(\left\{{}\begin{matrix}OA=OB=R\\MA=MB\left(gt\right)\end{matrix}\right.\) \(\Rightarrow OM\) là trung trực AB
\(\Rightarrow OM\perp AB\) tại H đồng thời \(HA=HB=\dfrac{AB}{2}\)
Trong tam giác vuông OMA: \(cos\widehat{AOM}=\dfrac{OA}{OM}=\dfrac{2}{2R}=\dfrac{1}{2}\Rightarrow\widehat{AOM}=60^0\)
\(\Rightarrow\widehat{AMO}=90^0-\widehat{AOM}=30^0\)
\(\Rightarrow\widehat{AMB}=2\widehat{AMO}=60^0\)
\(\Rightarrow\Delta AMB\) đều (tam giác cân có 1 góc bằng 60 độ)
Trong tam giác vuông OAH:
\(AH=OA.sin\widehat{AOM}=R.sin60^0=\dfrac{R\sqrt{3}}{3}\)
\(\Rightarrow AB=2AH=R\sqrt{3}\)
\(OH=OA.cos\widehat{AOM}=R.cos30^0=\dfrac{R}{2}\)
\(\Rightarrow HM=OM-OH=\dfrac{3R}{2}\)
\(\Rightarrow S_{ABM}=\dfrac{1}{2}HM.AB=\dfrac{3R^2\sqrt{3}}{4}\)
c.
BE là đường kính \(\Rightarrow\widehat{BAE}\) là góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{BAE}=90^0\Rightarrow AB\perp AE\)
Mà \(AB\perp OM\) (theo cm câu b)
\(\Rightarrow AE||OM\) (cùng vuông góc AB)


1. Kể lại một truyện đã biết (truyền thuyết, cổ tích) bằng lời văn của em: truyền thuyết Sơn Tinh, Thủy Tinh
“Âm... ầm...ầm”. Từng đợt sóng biển đập vào vách đá gợi cho em nhớ đến cuộc giao tranh ác liệt giữa Sơn Tinh và Thủy Tinh. Đây là một truyện rất hay mà em luôn nhớ từ thuở ấu thơ. Câu chuyện này đã được bà ngoại em kể vào những đêm trăng sáng khi mọi người ngồi xúm xít trước sân nhà.
Bà ke rằng vào thuở xa xưa, thời vua Hùng Vương thứ mười tám, vua có một người con gái tên là Mị Nương sắc đẹp như tiên giáng trần. Nhà vua rấtl thương con nên muốn tìm gả cho nàng một người chồng tài ba, tuấn tú.
Hai bài này góp thành 1 bài luôn nhé!
Lệnh vua vừa ban ra, các chàng trai từ khắp nơi đều đổ về cầu hôn. Trong số đó, nổi bật nhất là hai chàng trai Sơn Tinh và Thủy Tinh. Sơn Tinh dời núi Ba Vì. Chàng vừa tuấn tú lại vừa tài giỏi khác thường: chỉ tay về phía đông, phía đông biến thành đồng lúa xanh; chỉ tay về phía tây, phía tây mọc lên hàng dãy núi. Còn Thủy Tinh ở tận miền biển Đông, tài giỏi cũng không kém: gọi gió, gió đến; hô mưa, mưa về. Cả hai cùng ngang sức ngang tài và đều xứng đáng với Mị Nương.
Vua Hùng rất băn khoăn không biết chọn ai, bỏ ai. Vua liền triệu tập các quan vào bàn bạc nhưng cũng chẳng có ai nghĩ ra một kế gì hay. Cuối cùng, vua nghĩ ra được một cách và cho vời hai chàng trai vào mà phán rằng:
- Ta đều vừa ý cả hai người nhưng ta chỉ có một người con gái. Vậy vào rạng sáng ngày mai ai mang lễ vật đến trước thì ta gả con gái cho. Lễ cưới phải có đủ: một trăm ván cơm nếp, hai trăm tệp bánh chưng voi chín ngà, gà chín cựa, ngựa chín hồng mao.
Mới sáng sớm tinh mơ, Sơn Tinh đã đem đầy đủ lễ vật đến trước. Vua Hùng giữ đúng lời hứa liền gả Mị Nương cho Sơn Tinh và hai vợ chồng đưa nhau về núi.
Thủy Tinh mang lễ vật đến sau nên không cưới được vợ. Tức giận vô cùng, Thủy Tinh liền đùng đùng mang quân đuổi theo quyết cướp dược Mị Nương. Khi thây vợ chồng Sơn Tinh lên núi, Thủy Tinh hô mưa, gọi gió, làm thành giông bão, sấm sét rung chuyển cả đất trời, dâng nưởc sông lên cuồn cuộn. Nước ngập lúa ngập đồng, ngập nhà, ngập cửa..
Sơn Tinh không nao núng một chút nào. Một mặt, chàng dùng phép bốc cao từng quả đồi, dời từng dẫy núi để ngăn chặn dòng nước lũ. Nước dâng cao bao nhiêu, Sơn Tinh lại làm cho đồi núi mọc cao lên bấy nhiêu. Mặt khác, chàng tung ra đội quân sư tử, voi, cọp báo... để chống lại đoàn quân thuồng luồng, cá, tôm, cua... của Thủy Tinh. Hai bên đánh nhau ác liệt hết ngày này qua ngày khác ròng rã suốt mấy tháng liền. Thiệt hại người và của vô số kể. Cuối cùng, Thủy Tinh cũng đành thua trận rút quân về biển.
Với lòng hận thù triền miên nên từ đó về sau không năm nào Thủy Tinh không làm mưa bão, dâng nước lên để đánh Sơn Tinh, gây nên cảnh lụt lội, phá hoại nhà cửa, mùa màng của nước ta. Song, lần nào cũng vậy, Thủy Tinh lua thua trận và đành phải rút lui.
Kể xong câu chuyện, bà âu yếm xoa đầu em và nói: “Cuộc chiến giữa Sơn Tinh và Thủy Tinh thật ác liệt phải không các cháu? Hình ảnh này đã giải thích hiện tượng bão lụt xảy ra hằng năm suốt mùa mưa ở khăp vùng đồng bằng Bắc Bộ. Ngoài ra, truyện còn nói lên ước mơ của ngươi dân muốn chiến thắng bão lụt để bảo vệ cuộc sống lao dộng của mình. Các cháu có hiểu không?”
1. Kể một câu chuyện em thích bằng lời văn của em.

- Nói mỗi lông hút là một tế bào vì mỗi lông hút đều có những thành phần đặc trưng của 1 tế bào như vách tế bào , màng sinh chất , chất tế bào , nhân , không bào ,.....
- Lông hút không tồn tại mãi , đến một thời gian nào đó nó sẽ rụng và được thay thế bởi một lông hút khác .

Bài 70. ( trang 30 ) Viết các số: 987; 2564; abcde dưới dạng tổng các lũy thừa của 10.
Bài 73 : ( trang 32 )Giải: 987 = 9 . 102 + 8 . 10 + 7;
2564 = 2 . 103 + 5 . 102 + 6 . 10 + 4;
abcde= a . 104 + b . 103 + c . 102 + d . 10 + e
a) 5 . 42 – 18 : 32 = 5 . 16 - 18 : 9 = 80 - 2 = 78;
b) 33 . 18 – 33 . 12 = 27 . 18 - 27 . 12 = 486 - 324 = 162;
Lưu ý. Có thể áp dụng tính chất phân phối của phép nhân đối với phép cộng như sau:
33 . 18 – 33 . 12 = 33 (18 - 12) = 27 . 6 = 162;
c) 39 . 213 + 87 . 39 = 39 . (213 + 87) = 39 . 300 = 11700;
d) 80 – [130 – (12 – 4)2] = 80 - (130 - 82) = 80 - (130 - 64) = 80 - 66 = 14.
Bài 74 ( trang 32 ) a) 541 + (218 - x) = 735
Suy ra 218 - x = 735 - 541
218 - x = 194.
x = 218 - 194.
Vậy x = 24.
b) 5(x + 35) = 515
suy ra x + 35 = 515 : 5
x + 35 = 103.
x = 103 - 35 =68.
c) Từ 96 - 3(x + 1) = 42
suy ra 3(x + 1) = 96 - 42
3(x + 1)= 54.
x + 1 = 18.
x = 18 - 1
Vậy x = 17.
d) Từ 12x - 33 = 32 . 33
12x - 33 = 243
12x = 243 + 33
12x = 276
x = 276 : 12
Vậy x = 23.
Ko bt có phải bài bạn cần ko nx nhưng mong nó giúp được bn
Hok tốt
# MissyGirl #

Bài 3:
b: Xét ΔABC có
I là trung điểm của BC
IK//AC
Do đó: K là trung điểm của AB
Xét ΔABC có
I là trung điểm của BC
IH//AB
Do đó: H là trung điểm của AC
Xét ΔABC có
K là trung điểm của AB
H là trung điểm của AC
Do đó: HK là đường trung bình của ΔABC
Suy ra: HK//BC
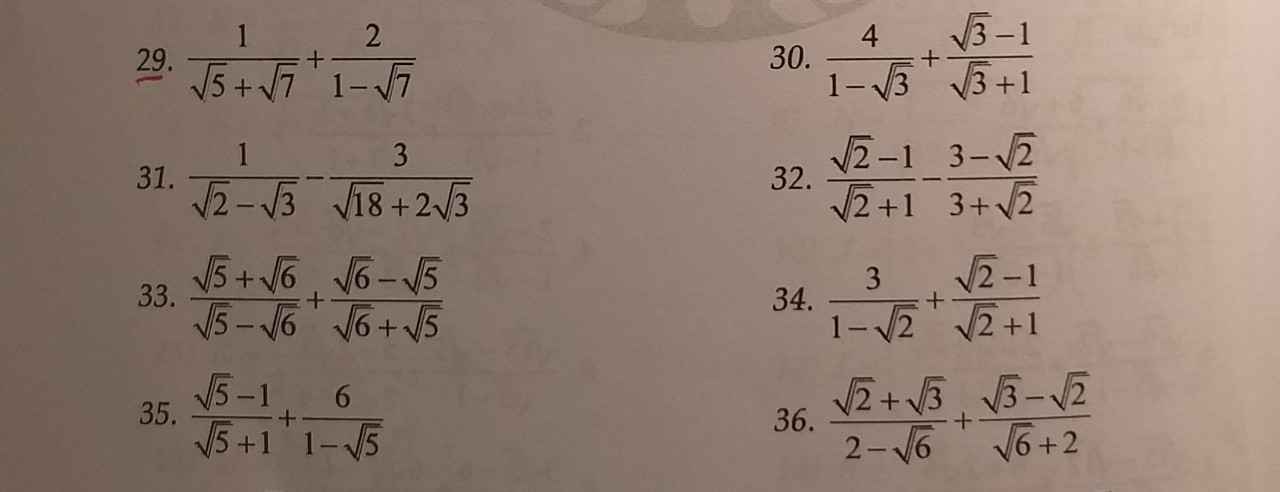




c, \(C=\left(2\sqrt{3}-5\sqrt{27}+4\sqrt{12}\right):\sqrt{3}\)
<=> \(C=\left(2\sqrt{3}-15\sqrt{3}+8\sqrt{3}\right):\sqrt{3}\)
<=> \(C=-5\sqrt{3}:\sqrt{3}=-5\)
e. \(\left(\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{5}}\right)^2\)
\(=3-\sqrt{5}+3+\sqrt{5}+2\sqrt{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}\)
\(=6+2\sqrt{9-5}\)
\(=6+4=10\)
b. \(\left(\sqrt{3}+2\right)^2-\sqrt{75}\)
\(=3+4\sqrt{3}+4-5\sqrt{3}\)
\(=7-\sqrt{3}\)
d. \(\left(1+\sqrt{3}-\sqrt{2}\right)\left(1+\sqrt{3}+\sqrt{2}\right)\)
\(=\left(1+\sqrt{3}\right)^2-2\)
\(=1+2\sqrt{3}+3-2\)
\(=2+2\sqrt{3}\)
f. \(\sqrt{\left(\sqrt{3}+2\right)^2}-\sqrt{\left(\sqrt{3}-2\right)^2}\)
\(=\left|\sqrt{3}+2\right|-\left|\sqrt{3}-2\right|\)
\(=\sqrt{3}+2-2+\sqrt{3}\)
\(=2\sqrt{3}\)
c: Ta có: \(C=\left(2\sqrt{3}-5\sqrt{27}+4\sqrt{12}\right):\sqrt{3}\)
\(=\left(2\sqrt{3}-5\cdot3\sqrt{3}+4\cdot2\sqrt{3}\right):\sqrt{3}\)
\(=2-15+8=-5\)
d: Ta có: \(D=\left(\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{5}}\right)^2\)
\(=3-\sqrt{5}+3+\sqrt{5}+2\cdot\sqrt{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}\)
\(=6+2\cdot2=10\)