Trong mặt phẳng Oxy cho đường thẳng d có phương trình \(x+y-2=0\). Hãy viết phương trình của đường thẳng d' là ảnh của d qua phép quay tâm O góc \(45^0\) ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Dễ thấy d chứa điểm H(1;1) và OH ⊥ d. Gọi H' là ảnh của H qua phép quay tâm O góc 45 o thì H ′ = ( 0 ; 2 ) . Từ đó suy ra d' phải qua H' và vuông góc với OH'. Vậy phương trình của d' là y = 2 .

Đáp án D
Ta có V I , 1 2 biến M 0 ; 2 ∈ d thành M ' x ' ; y ' thì I M ' → = 1 2 I M → ⇔ x ' = − 1 2 y ' = 1 2
V I , 1 2 biến đường thẳng d thành đường thẳng đi qua M ' − 1 2 ; 1 2 , có cùng vtpt 1 ; 1 và có phương trình là x + 1 2 + y − 1 2 = 0 ⇔ x + y = 0
Phép quay tâm O góc quay − 45 ° biến điểm N x ; y thuộc đường thẳng x + y = 0 thành điểm
N ' x ' ; y ' ∈ d ' ⇒ x = x ' cos 45 ° − y ' sin 45 ° y = x ' sin 45 ° + y ' cos 45 ° ⇒ x = 2 2 x ' − y ' y = 2 2 x ' + y ' *
Thay (*) vào x + y = 0 ta được x ' = 0 ⇒ d ' : x = 0

Đáp án D
Ta có V I , 1 2 biến M 0 ; 2 ∈ d thành M ' x ' ; y ' thì I M ' → = 1 2 I M → ⇔ x ' = − 1 2 y ' = 1 2
V I , 1 2 biến đường thẳng d thành đường thẳng đi qua M ' − 1 2 ; 1 2 , có cùng vtpt 1 ; 1 và có phương trình là x + 1 2 + y − 1 2 = 0 ⇔ x + y = 0
Phép quay tâm O góc quay − 45 ° biến điểm N x ; y thuộc đường thẳng x + y = 0 thành điểm
N ' x ' ; y ' ∈ d ' ⇒ x = x ' cos 45 ° − y ' sin 45 ° y = x ' sin 45 ° + y ' cos 45 ° ⇒ x = 2 2 x ' − y ' y = 2 2 x ' + y ' *
Thay * vào x + y = 0 ta được x ' = 0 ⇒ d ' : x = 0

Lấy A(3;9) thuộc (d)
Theo đề, ta có:
\(\left\{{}\begin{matrix}x_{A'}+3=0\\y_{A'}+9=0\end{matrix}\right.\Leftrightarrow A'\left(-3;-9\right)\)
Vì (d1)//(d) nên (d1): 5x-2y+c=0
Thay x=-3 và y=-9 vào (d1), tađược:
c+5*(-3)-2*(-9)=0
=>c-15+18=0
=>c=-3

Giả sử M 1 = D I ( M ) và M ′ = Q O ; − 90 ο ( M 1 ) . Ta có
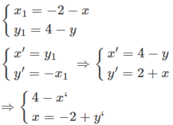
Thế (x;y) theo (x′;y′) vào phương trình d ta có:
3(y′ − 2) − (4 − x′) – 3 = 0 ⇔ x′ + 3y′ − 13 = 0
Vậy phương trình d’ là x + 3y – 13 = 0.



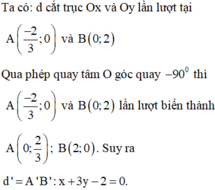

Dễ thấy d chứa điểm \(H\left(1;1\right)\) và \(OH\perp d\). Gọi H' là ảnh của H qua phép quay tâm O góc \(45^0\) thì \(H=\left(0;\sqrt{2}\right)\)
Từ đó suy ra d' phải qua H' và vuông góc với O'. Vậy phương trình của d' là \(y=\sqrt{2}\)