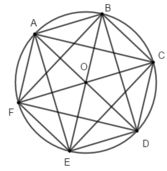
Cho lục giác đều ABCDEF. Chọ hệ tọa độ \(\left(O;\overrightarrow{i};\overrightarrow{j}\right)\), trong đó O là tâm của lục giác đều, hai vectơ \(\overrightarrow{i}\) và \(\overrightarrow{OD}\) cùng hướng, \(\overrightarrow{j}\) và \(\overrightarrow{EC}\) cùng hướng. Tính tọa độ các đỉnh của lục giác biết độ dài cạnh của lục giác là 6 ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


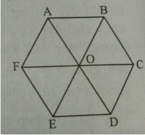
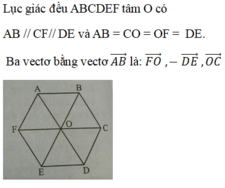
Do ABCDEF là lục giác đều tâm O nên AB = BC = CD= DE = EF = FA = OC.
Trên hình có tất cả 12 đoạn thẳng bằng nhau và bằng OC, tạo thành 24 vectơ có độ dài bằng OC. Trừ ra vectơ O C → còn lại 23 vectơ.
Chọn D.

Chọn đáp án A.
Ta có, đường tròn (O) ngoại tiếp lục giác đều ABCDEF nên
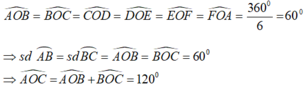

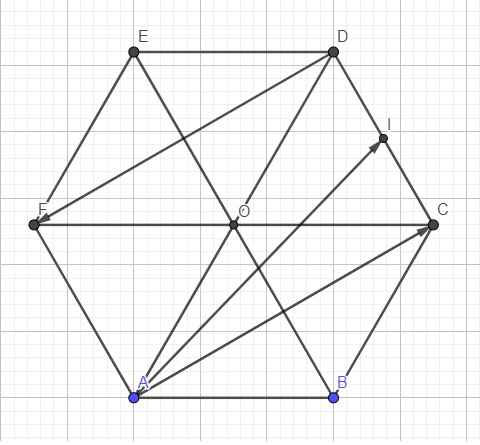
\(T=\left|\overrightarrow{DF}\right|=\left|\overrightarrow{DE}+\overrightarrow{EF}\right|\Rightarrow T^2=DE^2+EF^2+\overrightarrow{DE}.\overrightarrow{EF}\)
\(=a^2+a^2+a.a.cos60^0=3a^2\)
\(\Rightarrow\left|\overrightarrow{DF}\right|=a\sqrt{3}\)
\(AC=FD\Rightarrow\left|\overrightarrow{AC}\right|=a\sqrt{3}\)
\(P=\left|\overrightarrow{AI}\right|=\left|\dfrac{1}{2}\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{AC}\right|\Rightarrow P^2=\dfrac{1}{4}\left(AD^2+AC^2+2\overrightarrow{AD}.\overrightarrow{AC}\right)\)
\(=\dfrac{1}{4}\left(4a^2+3a^2+2.2a.a\sqrt{3}.cos30^0\right)=\dfrac{11}{2}a^2\)
\(\Rightarrow\left|\overrightarrow{AI}\right|=\dfrac{a\sqrt{22}}{2}\)

Phép quay tâm O góc quay - 60 o biến tam giác AFD thành tam gics ABE.
Đáp án C
TenAnh1 A = (-4.3, -5.94) A = (-4.3, -5.94) A = (-4.3, -5.94) B = (11.06, -5.94) B = (11.06, -5.94) B = (11.06, -5.94)
Do các tam giác OAB, OCD, OED, OEF, OFA , OBC cùng là tam giác đều nên OA = OB = OC = OD = OE = OF = 6cm.
Do \(\overrightarrow{i}\) và \(\overrightarrow{OD}\) cùng hướng nên D(6;0), A (0;-6).
Áp dụng hệ thức lượng trong tam giác vuông ta được:\(EC=2.DC.sin60^o=2.6.\dfrac{\sqrt{3}}{2}=6\sqrt{3}\).
\(\overrightarrow{EC}\) cùng hướng với \(\overrightarrow{j}\) nên:
Suy ra \(y_B=y_C=3\sqrt{3}\); \(y_E=y_F=-3\sqrt{3}\).
Do BC = 6cm và BC // OD nên \(x_E=x_C=3;x_F=x_B=-3\).
Vậy \(A\left(-6;0\right);D\left(6;0\right);B\left(-3;3\sqrt{3}\right),C\left(3;3\sqrt{3}\right)\);\(E\left(3;-3\sqrt{3}\right)\)\(F\left(-3;-3\sqrt{3}\right)\) .