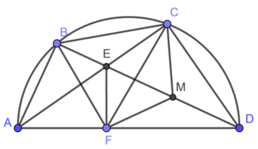
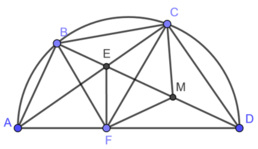
cho tứ giác ABCD nội tiếp đường tròn (O) đường kính AB. hai đường chéo AC và BD cắt nhau tại I. kẻ IE vuống góc với AB, chứng minh rằng :
a) tứ giác ADIE nội tiếp
b) tia DB là tia phân giác của góc CDE
c) trường hợp AB không song song với CD. chứng minh bốn điểm O,E,D,C cùng thuộc một đường tròn


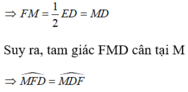
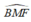 là góc ngoài tại đỉnh M của tam giác FMD nên:
là góc ngoài tại đỉnh M của tam giác FMD nên:
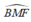 và
và 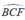 và cùng nhìn cạnh BF dưới một góc bằng nhau
và cùng nhìn cạnh BF dưới một góc bằng nhau
Em tự vẽ hình ra nháp để đối chiếu nhé!
a) Do đường tròn (O) đường kính AB nên \(\widehat{ADB} = 90^0\) mà \(\widehat{AHI} = 90^0\)
Suy ra tứ giác ADIE nội tiếp
b) Áp dụng góc nội tiếp nhìn cùng 1 cạnh bằng nhau cho 2 tứ giác nội tiếp ABCD và ADIE ta có:
\(\widehat{BDC} =\widehat{BAC}=\widehat{EDI} \)
Suy ra đpcm
c) Tam giác OAC cân tại O nên ta có:
\(\widehat{IOC}=2\widehat{OAC}=2\widehat{BDC}=\widehat{IDC}\) (theo câu b)
nên ta thu được tứ giác OECD nội tiếp!
cảm ơn nhìu ạ!! :)