Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét (O): E \(\in\) (O) (gt).
\(\Rightarrow\) \(\widehat{AEB}=90^o\) (Góc nội tiếp).
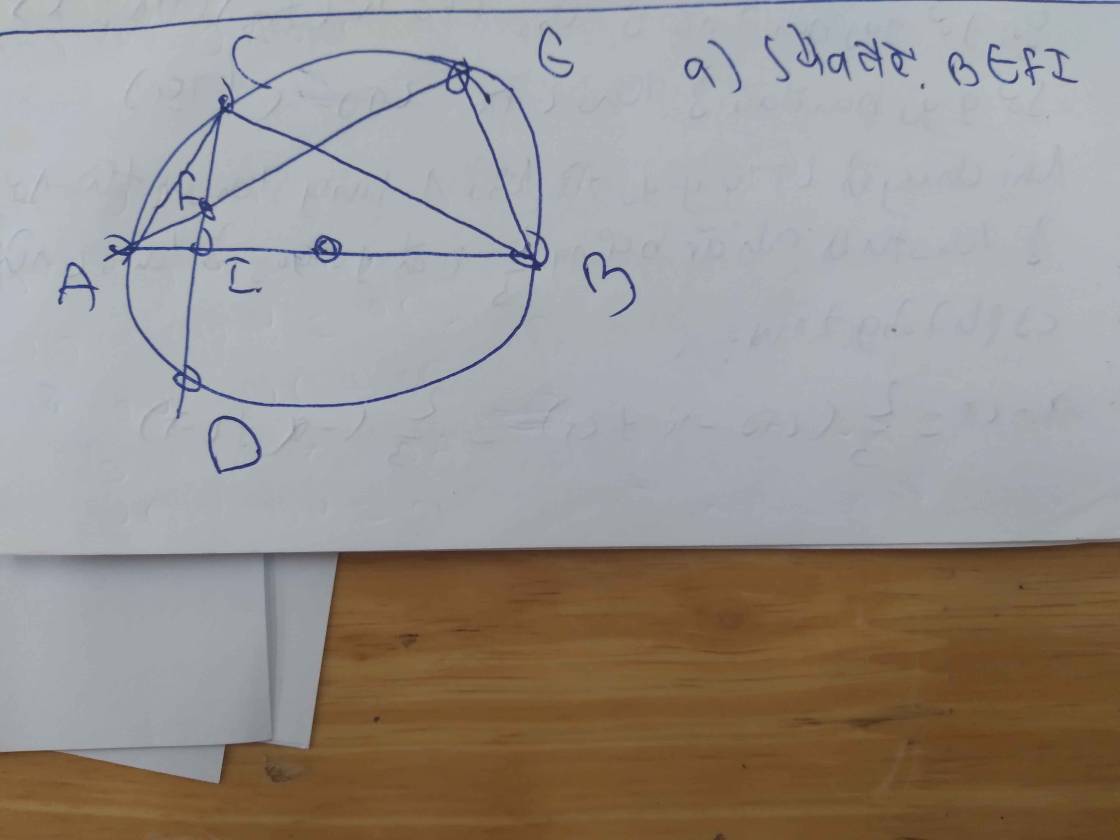
Xét tứ giác BEFI:
\(\widehat{AEB}+\widehat{CIB}=90^o+90^o=180^o.\)
Mà 2 góc này ở vị trí đối nhau.
\(\Rightarrow\) BEFI là tứ giác nội tiếp đường tròn.
b) Xét (O): \(CD\perp AB\) tại I (gt).
AB là đường kính; CD là dây (gt).
\(\Rightarrow\) I là trung điểm của CD.
Xét tam giác ACD:
AI là đường trung tuyến (I là trung điểm của CD).
AI là đường cao \(\left(AI\perp CD\right).\)
\(\Rightarrow\) Tam giác ACD cân tại A. \(\Rightarrow\) AC = AD (Tính chất tam giác cân).
Xét (O): AC = AD (cmt). \(\Rightarrow sđ\stackrel\frown{AC}=sđ\stackrel\frown{AD}.\)
Xét (O): \(\widehat{ACF}=\dfrac{1}{2}sđ\stackrel\frown{AD}\) (Góc nội tiếp).
Mà \(sđ\stackrel\frown{AD}=sđ\stackrel\frown{AC}\left(cmt\right).\)
\(\Rightarrow\) \(\widehat{ACF}=\dfrac{1}{2}sđ\stackrel\frown{AC}.\)
Mà \(\widehat{AEC}=\dfrac{1}{2}sđ\stackrel\frown{AC}\) (Góc nội tiếp).
\(\Rightarrow\widehat{ACF}=\widehat{AEC}.\)
Xét tam giác ACF và tam giác AEC:
\(\widehat{A}chung.\)
\(\widehat{ACF}=\widehat{AEC}\left(cmt\right).\)
\(\Rightarrow\) Tam giác ACF \(\sim\) Tam giác AEC (g - g).
\(\Rightarrow\) \(\dfrac{AC}{AE}=\dfrac{AF}{AC}\) (2 cạnh tương ứng tỉ lệ).
\(\Rightarrow AC^2=AE.AF\left(đpcm\right).\)


c) Có ACF = CBA (phụ ICB) . Trong (O) có ACF = CEF (chắn hai cung bằng nhau AC và cung AD) vậy ACF = CEF < 90 nên AC là tiếp tuyến của đường tròn ngoại tiếp tam giác CEF suay ra tâm của đường tròn đường tròn ngoại tiếp tam giác CEF thuộc đường vuông góc AC tại C nên Tâm thuộc AC cố định khi E thay đổi trên cung nhỏ BC

a) Tứ giác BEFI có: BFF = 90o (gt)
BEF = BEA = 90o
=> Tứ giác BEFI là nội tiếp đường tròn đường kính BF
b)
Vì \(AB\perp CD\)nên AC = AD
=> ACF = AEC
Xét tam giác ACF và tam giác AEC có gốc chung A và ACF = AEC
=> Tam giác ACF song song với tam giác AEC => \(\frac{AC}{AF}=\frac{AB}{AC}\)
=> AE . AF = AC2
c) Theo câu b) ta có: ACF = AEC = > AC là tiếp tuyến của đường tròn ngoại tiếp của tam giác CEF (1)
Mặt khác, ta có: ACB = 90o (góc nội tiếp chứa đường tròn)
\(\Rightarrow AC\perp CB\)(2)
Từ (1) và (2) => CB chứa đường kính của đường tròn ngoại tiếp tam giác CEF, mà CB cố định nên tâm của đường tròn ngoại tiếp tam giác CEF thuộc CB cố định E thay đổi trên cung nhỏ BC.

Ta có: ˆACD=900ACD^=900 (góc nội tiếp chắn nửa đường tròn đường kính AD)
Xét tứ giác DCEF có:
ˆACD=900ACD^=900 (cm trên)
ˆEFD=900EFD^=900 (vì EF⊥ADEF⊥AD (gt))
⇒ˆACD+ˆEFD=1800⇒ACD^+EFD^=1800
=> Tứ giác DCEF là tứ giác nội tiếp đường tròn (đpcm).
b) Vì tứ giác DCEF là tứ giác nội tiếp (chứng minh câu a)
⇒ˆC1=ˆD1⇒C1^=D1^ (góc nội tiếp cùng chắn cung EF) (1)
Mà ⇒ˆC2=ˆD1⇒C2^=D1^ (góc nội tiếp cùng chắn cung AB) (2)
Từ (1) và (2) ⇒ˆC1=ˆC2⇒C1^=C2^
⇒⇒ CA là tia phân giác của ˆBCFBCF^ (đpcm)
k đúng hộ

a) Xét (O) có
ΔACD nội tiếp đường tròn(A,C,D\(\in\)(O))
AD là đường kính(gt)
Do đó: ΔACD vuông tại C(Định lí)
Suy ra: AC\(\perp\)CD tại C
hay \(EC\perp CD\) tại C
Xét tứ giác ECDF có
\(\widehat{EFD}\) và \(\widehat{ECD}\) là hai góc đối
\(\widehat{EFD}+\widehat{ECD}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ECDF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

a: Xét (O) có
ΔAEB nội tiếp
AB là đường kính
Do đó: ΔAEB vuông tại E
Xét tứ giác BEFI có \(\widehat{BEF}+\widehat{BIF}=90^0+90^0=180^0\)
nên BEFI là tứ giác nội tiếp
b: Xét ΔAIF vuông tại I và ΔAEB vuông tại E có
\(\widehat{EAB}\) chung
Do đó: ΔAIF~ΔAEB
=>\(\dfrac{AI}{AE}=\dfrac{AF}{AB}\)
=>\(AI\cdot AB=AF\cdot AE\)