Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cô hướng dẫn nhé. :)
Tứ giác AIDE nội tiếp đường tròn đường kính AI.
b. Do câu a ta có AIDE là tứ giác nội tiếp nên gó IDE = góc IAE. Lại có góc IAE = góc CDB. Từ đó suy ra DB là tia phân giac góc CDE.
c. Ta thấy góc CDE = 2 góc CAB (Chứng minh b). Lại có góc COB = 2 góc CAB. Từ đó suy ra góc CDE = góc COB. Hay OEDC là tứ giác nội tiếp ( Góc ngoài ở đỉnh bằng góc đối diện )
Chúc em học tốt ^^

B1, a, Xét tứ giác AEHF có: góc AFH = 90o ( góc nội tiếp chắn nửa đường tròn)
góc AEH = 90o (góc nội tiếp chắn nửa đường tròn )
Góc CAB = 90o ( tam giác ABC vuông tại A)
=> tứ giác AEHF là hcn(đpcm)
b, do AEHF là hcn => cũng là tứ giác nội tiếp => góc AEF = góc AHF ( hia góc nội tiếp cùng chắn cung AF)
mà góc AHF = góc ACB ( cùng phụ với góc FHC)
=> góc AEF = góc ACB => theo góc ngoài tứ giác thì tứ giác BEFC là tứ giác nội tiếp (đpcm)
c,gọi M là giao điểm của AI và EF
ta có:góc AEF = góc ACB (c.m.t) (1)
do tam giác ABC vuông tại A và có I là trung điểm của cạng huyền CB => CBI=IB=IA
hay tam giác IAB cân tại I => góc MAE = góc ABC (2)
mà góc ACB + góc ABC + góc BAC = 180o (tổng 3 góc trong một tam giác)
=> ACB + góc ABC = 90o (3)
từ (1) (2) và (3) => góc AEF + góc MAE = 90o
=> góc AME = 90o (theo tổng 3 góc trong một tam giác)
hay AI uông góc với EF (đpcm)

1) Hình vẽ câu 1) đúng
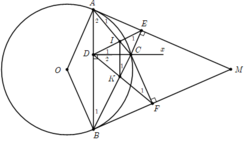
Ta có A E C ^ = A D C ^ = 90 0 ⇒ A E C ^ + A D C ^ = 180 0 do đó, tứ giác ADCE nội tiếp.
2) Chứng minh tương tự tứ giác BDCF nội tiếp.
Do các tứ giác A D C E , B D C F nội tiếp nên B 1 ^ = F 1 ^ , A 1 ^ = D 1 ^
Mà AM là tiếp tuyến của đường tròn (O) nên A 1 ^ = 1 2 s đ A C ⏜ = B 1 ^ ⇒ D 1 ^ = F 1 ^ .
Chứng minh tương tự E 1 ^ = D 2 ^ . Do đó, Δ C D E ∽ Δ C F D g.g
3) Gọi Cx là tia đối của tia CD
Do các tứ giác A D C E , B D C F nội tiếp nên D A E ^ = E C x ^ , D B F ^ = F C x ^
Mà M A B ^ = M B A ^ ⇒ E C x ^ = F C x ^ nên Cx là phân giác góc E C F ^ .
4) Theo chứng minh trên A 2 ^ = D 2 ^ , B 1 ^ = D 1 ^
Mà A 2 ^ + B 1 ^ + A C B ^ = 180 0 ⇒ D 2 ^ + D 1 ^ + A C B ^ = 180 0 ⇒ I C K ^ + I D K ^ = 180 0
Do đó, tứ giác CIKD nội tiếp ⇒ K 1 ^ = D 1 ^ mà D 1 ^ = B 1 ^ ⇒ I K / / A B

a) Xét (O) có
ΔACD nội tiếp đường tròn(A,C,D\(\in\)(O))
AD là đường kính(gt)
Do đó: ΔACD vuông tại C(Định lí)
Suy ra: AC\(\perp\)CD tại C
hay \(EC\perp CD\) tại C
Xét tứ giác ECDF có
\(\widehat{EFD}\) và \(\widehat{ECD}\) là hai góc đối
\(\widehat{EFD}+\widehat{ECD}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ECDF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

Em tự vẽ hình ra nháp để đối chiếu nhé!
a) Do đường tròn (O) đường kính AB nên \(\widehat{ADB} = 90^0\) mà \(\widehat{AHI} = 90^0\)
Suy ra tứ giác ADIE nội tiếp
b) Áp dụng góc nội tiếp nhìn cùng 1 cạnh bằng nhau cho 2 tứ giác nội tiếp ABCD và ADIE ta có:
\(\widehat{BDC} =\widehat{BAC}=\widehat{EDI} \)
Suy ra đpcm
c) Tam giác OAC cân tại O nên ta có:
\(\widehat{IOC}=2\widehat{OAC}=2\widehat{BDC}=\widehat{IDC}\) (theo câu b)
nên ta thu được tứ giác OECD nội tiếp!
cảm ơn nhìu ạ!! :)