cho 2 tia Ax và By cố định sông song và cùng chiều điểm M di động trên tia Ax và điểm N di động trên tia By sao cho \(\frac{AM}{BN}=\frac{1}{2}\) chứng minh đường thẳng Mn điq ua 1 điểm cố định(vẽ hộ hình)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


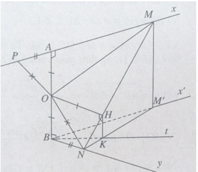
Theo giả thiết ta có M và N là hai điểm di động lần lượt trên hai tia Ax và By sao cho AM + BN = MN.
a) Kéo dài MA một đoạn AP = BN, ta có MP = MN và OP = ON.
Do đó ΔOMP = ΔOMN (c.c.c)
⇒ OA = OH nên OH = a.
Ta suy ra HM = AM và HN = BN.
b) Gọi M’ là hình chiếu vuông góc của điểm M trên mặt phẳng (Bx’, By) ta có:
HK // MM’ với K ∈ NM’.
Do đó đối với tam giác BNM’ đường thẳng BK là phân giác của góc (x'By) .
c) Gọi (β) là mặt phẳng (AB, BK). Vì HK // AB nên HK nằm trong mặt phẳng (β) và do đó H thuộc mặt phẳng (β). Trong mặt phẳng (β) ta có OH = a. Vậy điểm H luôn luôn nằm trên đường tròn cố định, đường kính AB và nằm trong mặt phẳng cố định (β) = (AB, BK)

câu a
Gọi H là chân đường vuông góc hạ từ M xuống tia phân giác ^BAC. Tam giác ADE có AH vừa là phân giác vùa là đường cao nên cân tại A.
Qua B vẽ BF//CE (F thuộc DE) => tam giác BDF cân tại B => BD = BF (1)
Mặt khác xét 2 tam giác BMF và CME có : BM = CM; ^BMF = ^CME ( đối đỉnh); ^MBF = ^MCE ( so le trong) => tam giác BMF = tg CME => BF = CE (2)
Từ (1) và (2) => đpcm
mấy câu còn lại bó tay

a: Sửa đề:I là chân đường cao kẻ từ O xuống AB. Chứng minh H,O,K thẳng hàng
Xét tứ giác AHOI có
\(\widehat{AHO}+\widehat{AIO}=180^0\)
=>AHOI là tứ giác nội tiếp
=>\(\widehat{HOI}+\widehat{HAI}=180^0\)
Xét tứ giác OIBK có \(\widehat{OIB}+\widehat{OKB}=180^0\)
=>OIBK là tứ giác nội tiếp
=>\(\widehat{IOK}+\widehat{IBK}=180^0\)
AH//BK
=>\(\widehat{HAI}+\widehat{KBI}=180^0\)
\(\widehat{HOI}+\widehat{KOI}\)
\(=180^0-\widehat{HAI}+180^0-\widehat{KBA}\)
\(=360^0-180^0=180^0\)
=>H,O,K thẳng hàng
b: Xét ΔAHO vuông tại H và ΔAIO vuông tại I có
AO chung
\(\widehat{HAO}=\widehat{IAO}\)
Do đó: ΔAHO=ΔAIO
=>AH=AI
Xét ΔOIB vuông tại I và ΔOKB vuông tại K có
BO chung
\(\widehat{IBO}=\widehat{KBO}\)
Do đó: ΔOIB=ΔOKB
=>BI=BK
AH+BK=AI+IB=AB không đổi
\(\widehat{OBA}+\widehat{OAB}=\dfrac{1}{2}\left(\widehat{HAB}+\widehat{KBA}\right)\)
\(=\dfrac{1}{2}\cdot180^0=90^0\)
=>ΔOAB vuông tại O
=>ΔOAB nội tiếp đường tròn đường kính BA
\(\widehat{HIK}=\widehat{HIO}+\widehat{KIO}\)
\(=\widehat{HAO}+\widehat{OBK}\)
\(=\widehat{OAB}+\widehat{OBA}=90^0\)
=>ΔHIK vuông tại I
=>ΔHIK nội tiếp đường tròn đường kính HK

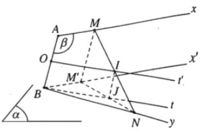
a) Gọi (β) là mặt phẳng xác định bởi hai đường thẳng AB và Ax
Do Ax // (α) nên (β) sẽ cắt (α) theo giao tuyến Bx’ song song với Ax.
Ta có M’ là điểm chung của (α) và (β) nên M’ thuộc Bx’.
Khi M trùng A thì M’ trùng B nên tập hợp M’ là tia Bx’.
Ta có tứ giác ABM’M là hình bình hành nên BM’ = AM = BN.
Tam giác BM’N cân tại B.
Suy ra trung điểm I của cạnh đáy NM’ thuộc phân giác trong Bt của góc B trong tam giác cân BNM’. Dễ thấy rằng Bt cố định.
Gọi O là trung điểm của AB. Trong mặt phẳng (AB, Bt), tứ giác OBIJ là hình bình hành nên I J → = B O → . Do đó I là ảnh của J trong phép tịnh tiến theo vectơ B O → . Vậy tập hợp I là tia Ot’ song song với Bt.

