Giá trị lớn nhất của biểu thức là A= 6/x^2+3 là Amax=
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 1 2017
Để \(A=\frac{6}{x^2+3}\) đạt gtln <=> \(x^2+3\) đạt gtnn
\(x^2\ge0\Rightarrow x^2+3\ge3\)
Dấu "=" xay ra <=> x2 = 0 => x = 0
Vậy gtnn của A là \(\frac{6}{0+3}=2\) tại x = 0
DP
7 tháng 3 2015
Để A lớn nhất thì 6/x2 phải lớn nhất mà 6/x2 lớn nhất thì x2 phải nhỏ nhất với x \(\varepsilon\) N => x = 1
Ta có: A = 6/x2 + 3 = 6/1 + 3= 6 + 3 = 9
21 tháng 2 2018
1. a, => -12x+60+21-7x = 5
=> 81 - 19x = 5
=> 19x = 81 - 5 = 76
=> x = 76 : 19 = 4
Tk mk nha
QH
0
VN
20 tháng 1 2017
Làm khâu rút gọn thôi
\(=\frac{15}{x+2}+\frac{42}{3x+6}\)
\(=\frac{15}{x+2}+\frac{42}{3\left(x+2\right)}\)
\(=\frac{3.15+42}{3\left(x+2\right)}\)
\(=\frac{87}{3\left(x+2\right)}\)
\(=\frac{29}{x+2}\)
VN
20 tháng 1 2017
Câu b có phải để tử chia hết cho mẫu không nhỉ? Không chắc thôi để ngkh làm
CM
14 tháng 6 2018
P có giá trị số lớn nhất khi (x - 6 ) có giá trị bé nhất.
Giá trị bé nhất của (x - 6 ) là: x - 6 = 1
x = 1 + 6
x = 7
Khi đó giá trị số của biểu thức P là:
P = 2004 + 540 : ( 7 - 6 )
= 2004 + 540
= 2544
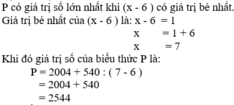
Ta có: \(x^2\ge0\)
\(\Rightarrow x^2+3\ge3\)
\(\Rightarrow\frac{1}{x^2+3}\ge\frac{1}{3}\)
\(\Rightarrow\frac{6}{x^2+3}\ge2\)
Dấu "=" xảy ra khi x = 0
Vậy AMax = 2 khi x = 0