Tìm các số x,y,z sao cho x:y:z =4:5:6 và x2 -2y2 +z2=18
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
3
MT
2 tháng 7 2015
x:y:z= 4:5:6
=>x/4=y/5=z/6
=>x2/16=2y2/50=z2/36
áp dụng tính chất của dãy tỉ số bằng nhau ta có:
x2/16=2y2/50=z2/36=x^2- 2y^2+ z^2/16-50+36=18/2=9
suy ra x2/16=9 =>x2=144 =>x=12 hoặc x=-12
2y2/50=9 =>y2=225 => y=15 hoặc y=-15
z2/36=9 =>z2=324 =>z=18 hoặc z=-18
8 tháng 8 2017
\(x:y:z=4:5:6\Rightarrow\frac{x}{4}=\frac{y}{5}=\frac{z}{6}\)và x2 - 2y2 + z2 = 18
\(\Rightarrow\frac{x}{4}=\frac{x^2}{4^2}=\frac{x^2}{16}\)
\(\Rightarrow\frac{y}{5}=\frac{2y^2}{2.5^2}=\frac{2y^2}{50}\)
\(\Rightarrow\frac{z}{6}=\frac{z^2}{6^2}=\frac{z^2}{36}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{x^2}{16}=\frac{2y^2}{50}=\frac{z^2}{36}=\frac{x^2-2y^2+z^2}{16-50+36}=\frac{18}{2}=9\)
\(\frac{x^2}{16}=9\Rightarrow x^2=9.16=x^2=144\Rightarrow x=12\)
\(\frac{2y^2}{50}=9\Rightarrow2y^2=9.50=2y^2=450=y^2=450:2=y^2=225\Rightarrow y=15\)
\(\frac{z^2}{36}=9\Rightarrow z^2=9.36=z^2=324\Rightarrow z=18\)
Vậy......
4 tháng 8 2018
Đặt \(\frac{x}{2}=\frac{y}{3}=\frac{z}{5}=k\left(k\ne0\right)\)
\(\Rightarrow\hept{\begin{cases}x=2k\\y=3k\\z=5k\end{cases}}\)
Mà \(x^2-2y^2+z^2=44\)
\(\Rightarrow\left(2k\right)^2+2\left(3k\right)^2+\left(5k\right)^2=44\)
\(\Leftrightarrow4k^2-18k^2+25k^2=44\)
\(\Leftrightarrow k^2\left(4-18+25\right)=44\)
\(\Leftrightarrow k^2.11=44\)
\(\Leftrightarrow k^2=4\)
\(\Leftrightarrow\orbr{\begin{cases}k=2\\k=-2\end{cases}}\)
+) Với \(k=2\)thì \(\hept{\begin{cases}x=2k=4\\y=3k=6\\z=5k=10\end{cases}}\)
+) Với \(k=-2\)thì \(\hept{\begin{cases}x=2k=-4\\y=3k=-6\\z=5k=-10\end{cases}}\)
Vậy ...
15 tháng 11 2015
bài 2 :
ta có x:y:z=3:5:(-2)
=>x/3=y/5=z/-2
=>5x/15=y/5=3z/-6
áp dụng tc dãy ... ta có :
5x/15=y/5=3z/-6=5x-y+3z/15-5+(-6)=-16/4=-4
=>x/3=-=>x=-12
=>y/5=-4=>y=-20
=>z/-2=-4=>z=8
DN
2
AH
Akai Haruma
Giáo viên
22 tháng 11 2023
1.
Áp dụng tính chất dãy tỉ số bằng nhau:
$\frac{x}{5}=\frac{y}{7}=\frac{z}{10}=\frac{2x}{10}=\frac{y}{7}=\frac{z}{10}$
$=\frac{2x+y-z}{10+7-10}=\frac{-21}{7}=-3$
$\Rightarrow x=-3.5=-15; y=-3.7=-21; z=-3.10=-30$
AH
Akai Haruma
Giáo viên
22 tháng 11 2023
2.
Áp dụng tính chất dãy tỉ số bằng nhau:
$\frac{x}{3}=\frac{y}{4}=\frac{z}{6}=\frac{2x}{6}=\frac{4y}{16}=\frac{3z}{18}$
$=\frac{4y-2x+3z}{16-6+18}=\frac{-56}{28}=-2$
$\Rightarrow x=-2.3=-6; y=-2.4=-8; z=-2.6=-12$
NM
7 tháng 3 2021
Do vai trò bình đẳng của x, y, z trong phương trình,
trước hết ta xét x ≤ y ≤ z.
Vì x, y, z nguyên dương nên xyz ≠ 0, do x ≤ y ≤ z
=> xyz = x + y + z ≤ 3z => xy ≤ 3=> xy thuộc {1 ; 2 ; 3}.
Nếu xy = 1 => x = y = 1,
thay vào (2) ta có : 2 + z = z, vô lí.
Nếu xy = 2, do x ≤ y nên x = 1 và y = 2,
thay vào (2), => z = 3.Nếu xy = 3,
do x ≤ y nên x = 1 và y = 3,
thay vào (2), => z = 2.
Vậy nghiệm nguyên dương của phương trình (2) là các hoán vị của (1 ; 2 ; 3)
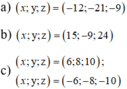
Ta có: x:y:z =4:5:6
⇒\(\dfrac{x}{4}=\dfrac{y}{5}=\dfrac{z}{6}\)
⇒\(\dfrac{x^2}{16}=\dfrac{2y^2}{50}=\dfrac{z^2}{36}\)
⇒\(\dfrac{x^2-2y^2+z^2}{16-50+36}=\dfrac{18}{2}=9\)
\(\dfrac{x}{4}=9\Rightarrow x=36\)
\(\dfrac{y}{5}=9\Rightarrow y=45\)
\(\dfrac{z}{6}=9\Rightarrow z=54\)