Chọn câu đúng . Giả sử \(\frac{x}{y}=4;x.y=9\) . Ngoài ra \(x\) lớn hơn hoặc bằng 0 . Khi đó (x;y) bằng :
A . (4 ; 1 ) B . (8;2) C. (3;3) D . (9;1) E . ( 6 ; \(\frac{3}{2}\))
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
13 tháng 2 2019
Đáp án cần chọn là: A
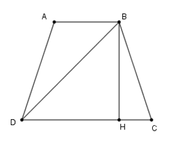
Kẻ BH ⊥ CD tại H.
Xét tam giác vuông BDH, theo định lý Pytago, ta có B D 2 = D H 2 + B H 2
Xét tam giác vuông CBH, theo định lý Pytago, ta có B C 2 = C H 2 + B H 2
Suy ra B D 2 - B C 2 = D H 2 + B H 2 - C H 2 + B H 2
= D H 2 - C H 2 = B H + D H × D H - B H = C D × A B
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 1 2024
Giả sử học sinh đó chọn x câu đúng (với \(0\le x\le10\)), như vậy sẽ có \(10-x\) câu sai
Số điểm học sinh đó đạt được là:
\(5x-2\left(10-x\right)=7x-20\)
Điểm dưới 1 \(\Rightarrow7x-20< 1\Rightarrow x< 3\)
Vậy học sinh đó trả lời đúng 0,1 hoặc 2 câu
Xác suất đúng khi chọn mỗi câu hỏi là 1/4 còn xác suất sai là 3/4 nên xác suất học sinh đó dưới 1 điểm là:
\(C_{10}^0.\left(\dfrac{1}{4}\right)^0.\left(\dfrac{3}{4}\right)^{10-0}+C_{10}^1.\left(\dfrac{1}{4}\right)^1.\left(\dfrac{3}{4}\right)^{10-1}+C_{10}^2.\left(\dfrac{1}{4}\right)^2.\left(\dfrac{3}{4}\right)^{10-2}=...\)
10 tháng 6 2017
Vì x < y nên \(\frac{a}{m}< \frac{b}{m}\) suy ra a < b
=> a + b > 2a => \(z=\frac{a+b}{2m}>\frac{2a}{2m}=\frac{a}{m}=x\) (1)
Từ a < b => a + b < 2b => \(z=\frac{a+b}{2m}< \frac{2b}{2m}=\frac{b}{m}=y\) (2)
Từ (1) ; (2) => x < z < y (đpcm)
(a, b, m ∈ Z; m > 0) và x < y. Hãy chứng minh nếu chọn 
thì ta có x < z < y.
7 tháng 9 2021
Chào bn , cảm ơn bạn đã bình luận . Nếu khó hiểu chỗ nào vui lòng nhắn tin cho mình
Trân trọng cảm ơn
22 tháng 8 2016
Ta có x = \(\frac{2a}{2m}\)< \(\frac{a+b}{2m}\)= z
y = \(\frac{2b}{2m}\)> \(\frac{a+b}{2m}\)= z
22 tháng 8 2016
Do x < y => a/m < b/m
=> a/m + a/m < a/m + b/m < b/m + b/m
=> 2x < a+b/m < 2y
=> x < a+b/m : 2 < 2y
=> x < a+b/m . 1/2 < y
=> x < a+b/2m < y
Chứng tỏ ...
NN
15 tháng 4 2020
Vì x<y nên a<b. Ta có \(x=\frac{a}{m}=\frac{2a}{2m},y=\frac{b}{m}=\frac{2b}{2m}\)
Chọn \(z=\frac{2a+1}{2m}\).Do 2a<2a+1 nên x<z(1)
Do a<b nên a+1 < b suy ra 2a+1< 2b
TA có 2a+1< 2a+2< 2b nên 2a+1<2b do đó z<y(2)
Từ (1),(2) suy ra x<z<y
15 tháng 4 2020
Ta có: x<y => \(\frac{a}{m}< \frac{b}{m}\)<=> a<b
Lại có:\(x=\frac{a}{m}=\frac{2a}{2m};y=\frac{b}{m}=\frac{2b}{2m}\)
vì a<b (a, b thuộc Z) <=> a+1 =< b hay 2a+2 =< 2b
=> 2a <2a+1<2a+2=<2b hay 2a<2a+1<2b
do đó: \(\frac{2a}{2m}< \frac{2+1}{2m}< \frac{2b}{2m}\)
=> x<y<z
Nguồn: loigiaihay.com
Từ giả thiết y = \(\frac{x}{4}\) và \(\frac{x^2}{4}=9\) => x = \(\sqrt{36}=6\left(x\ge0\right)\)
y=\(\frac{6}{4}=\frac{3}{2}\)
Vậy : E đúng
Hjhj
Anh thấy thường thường có 4 đáp án , liếc thấy cái cuối cùng đúng nên chọn D
:v