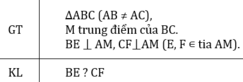
Cho tam giác ABC(AB\(\ne\)AC), tia Ax đi qua trung điểm M của BC. Kẻ BE và CF vuông góc với Ax(E thuộc Ax, F thuộc Ax). So sánh độ dài BE và CF
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 2 2021
xét tam giác vuông BEC có EM là đường trung tuyến ứng với cạnh huyền
suy ra EM = \(\frac{1}{2}\)BC (1)
xét tam giác vuông CFB có FM là đường trung tuyến ứng với cạnh huyền
suy ra FM = \(\frac{1}{2}\)BC (2)
từ (1) và (2) suy ra M là trung điểm EF
mà M là trung điểm của BC
từ 2 điều đó suy ra BECF là hình bình hành
suy ra BE = CF
VT
29 tháng 11 2014
Xét 2 TG vuông BME và CMF, ta có:
BM=CM(M là tđiểm BC); BME=CMF(2 góc đđ)
=>TG BME=TG CMF(cạnh huyền-góc nhọn)
=>BE=CF(2 cạnh tương ứng)
20 tháng 11 2017
Xét 2 TG vuông BME và CMF, ta có:
BM=CM(M là tđiểm BC); BME=CMF(2 góc đđ)
=>TG BME=TG CMF(cạnh huyền-góc nhọn)
=>BE=CF(2 cạnh tương ứng)
CM
26 tháng 8 2017
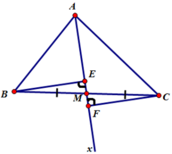
Hai tam giác vuông BME và CMF có
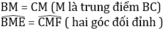
⇒ ΔBME = ΔCMF (cạnh huyền – góc nhọn)
⇒ BE = CF (hai cạnh tương ứng).
* Chú ý: Các em có thể suy nghĩ tại sao cần điều kiện AB ≠ AC ???
16 tháng 7 2017
Hai tam giác vuông BME, CMF có:
BM=MC(gt)
=
(đối đỉnh)
Nên ∆BME=∆CMF(cạnh huyền- góc nhọn).
Suy ra BE=CF.
16 tháng 7 2017
Vì tia Ax đi qua trung điểm M của BC => AM là đường trung tuyến của tam giác của tam giác ABC và BM = MC.
BE II CF vì 2 đường thẳng này cùng vuông góc với tia Ax(đl 1 bài từ vuông góc tới song song)
Xét tam giác BME và tam giác CMF có :
Góc EBM = Góc MCF(so le trong)
BM = MC.
BME = CMF(2 góc đối đỉnh)
=> 2 tam giác này bằng nhau( g.c.g)
=> BE = CF(2 cạnh tương ứng)
8 tháng 12 2021
Xét ΔBEM vuông tại E và ΔCFM vuông tại F có
MB=MC
\(\widehat{BME}=\widehat{CMF}\)
Do đó: ΔBEM=ΔCFM
19 tháng 12 2016
Ta có hình vẽ trên:
Xét 2 tam giác vuông MBE và tam giác MCF có:
BM = MC (gt)
góc M1 = góc M2 (đối đỉnh)
suy ra tam giác MBE = tam giác MCF (cạnh huyền - góc nhọn)
suy ra BE = CF (2 cạnh tương ứng)
Vậy BE = CF
S
22 tháng 11 2017
Xét \(\Delta BEM\) và \(\Delta CFM\) có:
\(\widehat{E}=\widehat{F}=90^o\)
MB = MC (gt)
\(\widehat{BME}=\widehat{CMF}\) (đối đỉnh)
Do đó \(\Delta BEM=\Delta CFM\) (cạnh huyền - góc nhọn)
=> BE = CF (2 cạnh t/ứ)
22 tháng 11 2017
Xét \(\Delta BEM\)và \(\Delta CFM\)
\(\widehat{E}=\widehat{F}=90^{ }\)độ
\(MB=MC\)( gt )
\(\widehat{BME}=CMF\)( đối đỉnh )
\(\Rightarrow\)\(\Delta BEM=\Delta CFM\)( g - c - g )
\(\Rightarrow\)\(BE=CF\)( 2 cạnh tương ứng bằng nhau )
QD
20 tháng 4 2017
Hai tam giác vuông BME, CMF có:
BM=MC(gt)
ˆBMEBME^=ˆCMFCMF^(đối đỉnh)
Nên ∆BME=∆CMF(cạnh huyền- góc nhọn).
Suy ra BE=CF.
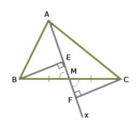
Ta có hình vẽ:
Δ CFM có: CFM + FMC + MCF = 180o
Δ EMB có: EMB + MBE + BEM = 180o
Mà CFM = MEB = 90o
FMC = BME (đối đỉnh) nên MCF = MBE
Xét Δ MCF và Δ MBE có:
MCF = MBE (cmt)
CM = BM (gt)
FMC = EMB (đối đỉnh)
Do đó, Δ MCF = Δ MBE (c.g.c)
=> CF = BE (2 cạnh tương ứng)
g-c-g mà bạn